Zadanie Wydi: Wykaż że długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny wtedy i tylko wtedy gdy trójkąt ten jest podobny do trójkąta o bokach 3, 4, 5.

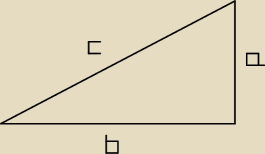
Jacek Karaśkiewicz: Ustalmy bez straty ogólności, że a ≤ b < c. Aby udowodnić równoważność, należy wykazać implikacje w obie strony. 1. "→" Jeżeli długości te tworzą ciąg arytmetyczny to musi być. b = a + r, c = b + r = a + 2r, , dla jakiegoś r ∈ R. Jeżeli trójkąt ten ma być podobny do trójkąta o bokach długości 3, 4, 5 to musimy mieć:

3		4		5
	=		=		= s, s ∈ R
a		b		c

3		4		5
	=		=		= s, s ∈ R
a		a + r		a + 2r

	3		4
Rzeczywiście, jeśli		=		to a = 3r i spełnia to drugą część równości,
	a		a + r

	4		5
czyli		=		.
	a + r		a + 2r

	1
Czyli mamy podobieństwo w skali 1r ( s =		).
	r

2. "←" Załóżmy, że nasz trójkąt o bokach długości a, b, c jest podobny do trójkąta o bokach długości 3, 4, 5. Czyli zachodzi:

3		4		5
	=		=		= s, dla jakiegoś s ∈ R.
a		b		c

Czyli mamy: a = ³_s, b = ⁴_s, c = ⁵_s. A więc istnieje takie r = ¹_s, że: b = a + r, c = b + r = a + 2r, czyli długości te tworzą ciąg arytmetyczny. Udowodnienie implikacji → oraz ← dowodzi równoważności.