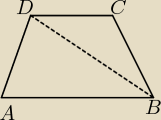
Geometria Nikusia: Zad 5 W trapezie ABCD w którym AB || DC oraz |AB|>|DC| przekątna DB zawiera się dwusiecznej kąta ABC.Wykaż , że |DC|=|BC|

Mila: ΔDBC jest równoramienny. Pomyśl dlaczego.

rumpek: Oznacz sobie kąt |∡B| = 2α, dwusieczna zatem podziel go na |∡ABD| = |∡CBD| = β. Kąt |∡BCD| będzie wynosił 180^o − 2β, ponieważ suma miar kątów przy jednym ramieniu w trapezie wynosi 180^o. Zatem możemy sobie oznaczyć kąt |∡BDC| = γ. I podstawiamy tylko: 180^o = β + γ + 180^o − 2β (180^o tyle wynosi suma miar kątów w trójkącie). 180^o = −β + γ + 180^o ⇒ 0 = −β + γ ⇔ γ = β. Czyli trójkąt BCD jest równoramienny, zatem długości |DC| i |BC| są sobie równe, c.n.u

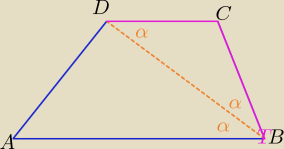
Eta: |<ABD|=|<DBC|= α −−− z własności dwusiecznej < BDC=<ABD −−− jako kąty naprzemianległe Trójkąt BCD jest równoramienny o ramionach |DC|= |BC| c.n.u.

rumpek:

Eta:

Nikusia: nie rozumiem jak to zapisać wszystko

Nikusia: to wreszcie jak mam to zrobic

pigor: ... sprawa jest prostsza niż się ... wydaje , bo z warunków zadania masz wszystko jak na ... tacy , że kąty naprzemianległe wewnętrzne i kąty dwusiecznej : ∡ ABD = ∡BDC = ∡DBC ⇒ |DC|=|BC| c.n.w. . ...

rumpek: Posty: Ety, Mili, i mój to jeden sposób więc nie wiem z czym problem Eta nawet rysunek pyknęła

pigor: ... pytanie nie na miejscu , delikatnie mówiąc, bo może byś poczytała i sama podjęła decyzje zgodną ze swoim poziomem , czyli odczuciem , dobrze , pozdrawiam . ...

Nikusia: już właśnie wiem wszystko Dzięki wielkie za taką ogromną pomoc

Eta: