P.parametryczna Tiamat: jak obliczyć postać parametryczną prostej? ;c mógłby mi ktoś wytłumaczyć, co po kolei robić? A(1,5) B(−1,−2)

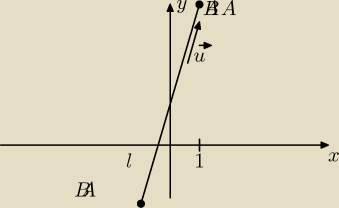
Aga1: A=(1,5)=(x__0,y₀) u→=BA→=[2,7]=[a,b] l; x=x₀+at y=y₀+bt, t∊R x=1+2t y=5+7t, t∊R Mam nadzieję, że tak.

Tiamat: Ok, próbuję to przeanalizować i zacięłam się na jednym: możesz mi wytłumaczyć skąd Ci wyszło [2,7]? Bo mi wyszło [3,6] i się zastanawiam jak to się stało:3

Godzio: To jest wektor BA, od współrzędnej A odejmujesz współrzędne B:: [1 − (−1), 5 − (−2)] = [2,7]

Aga1: AB→=[x_B−x_A, y_B−y_A] AB→=[−1−1, −2−5]=[−2−7] BA→=[2,7]

Tiamat: aha, już wiem, czemu tak wychodzi, napisałam na odwrót Przepraszam was, ale ma być: B(−2,−1), pospieszyłam się trochę za bardzo czyli teraz się zgadza: A−B: 1−(−2)=3 5−(−1)=6 ?

pigor: ... lub np. tak:

x−1		y−5		x−1		y−5		x−1		y−5
	=		⇔		=		= t ⇔		=		= t ⇔
−1−1		−2−5		−2		−7		2		7

x−1=2t i y−5=7t ⇔ x=1+2t i y=5+7t , t∊R ⇔ (x,y)=(1+2t, 5+7t) , t∊R . ...

Tiamat: Nie, to chyba juz mnie przerasta, wolę proste sposoby; ) Ok, czyli biorę potem dane z A? Dlaczego tak, a nie z B?

pigor: ...

Tiamat: No jak mam x=1+2t y=5+7t, t∊R to są tu użyte współrzędne z pkt A(1,5), dlaczego nie z B?:3

Aga1: Przelicz sobie, nie ma znaczenia, czy bierzesz A, czy B , czy obliczysz AB→, czy BA→ końcowy wynik powinien być taki sam.

pigor: ... ja chce ci tylko pokazać sedno problemu , czyli ... skąd taka, a nie inna postać , a jak nie chcesz, to oczywiście , twój ... biznes, pozdrawiam . ...

Aga1: Jak przekształcisz np do postaci kierunkowej to wynik będzie taki sam

Tiamat: ok, faktycznie wychodzi to samo, ale jak wcisnę tam x i y z B to chyba już nie?: x=−2+3t y=−1+6t Czy to obojętne co tam jest na początku a ważne tylko to przed t?