?
klo: Dana jest nierówność mx2+x+1=0. Dla jakich m:
− jednym z pierwiastków jest liczba 1
− liczba 1 zawiera się między pierwiastkami
25 mar 10:29
Alkain: 1*
f(1)=m1
2+1+1=0
m=−2
Nad drugim muszę chwile pomyśleć

25 mar 10:54
klo: dziękuję

za pomoc
25 mar 10:57
Alkain: m≠0
Δ>0
Δ=1
2−4m1>0
1>4m
−1=2m
Nie mam pomysłu jak to skończyć na pewno będzie jakiś przedział

25 mar 11:02
klo: nie za bardzo rozumiem dlaczego tak postępowałeś
25 mar 11:22
MQ: Liczysz Δ
Warunek Δ>0, zeby były dwa pierwiastki
Liczysz pierwiastki x1 i x2
Sprawdzasz warunek:
x1< 1 < x2
25 mar 11:26
klo: ale nic mi z tego nie wychodzi
25 mar 11:29
Aga1:
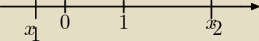
1∊(x
1,x
2)
x
1<1
x
2>1/*(−1)
x
1<1
−x
2<−1
−−−−−−−−−−−
x
1−x
2<0/*(−1)
x
2−x
1>0 /
2
(x
2−x
1)
2>0
(x
12+x
22)−2x
1x
2>0
(x
1+x
2)
2−4x
1x
2>0
25 mar 11:37
Aga1: Masz odpowiedź ?
25 mar 11:38
klo: znowu mi coś nie wyszło

25 mar 11:42
klo: wyszło mi że dla m<0
25 mar 11:44
klo: dobrze, czy źle?
25 mar 11:44
MQ:
| −1−√1−4m | | −1+√1−4m | |
| < 1 < |
|
|
| 2m | | 2m | |
−
√1−4m < 2m+1 <
√1−4m
25 mar 11:47
klo: a jak to dalej rozpisać?
25 mar 11:49
Aga1: MQ, a skąd wiesz, że m>0, bo mnożąc nierówność musiałeś zrobić takie założenie , gdyż nie
zmieniłeś kierunku nierówności.
25 mar 11:50
MQ: Trzeba rozbić na dwa przypadki: m>0 i m<0
25 mar 11:54
klo: ja już nic nie wiem
25 mar 11:59
MQ: m>0
2m+1<
√1−4m |
2
4m
2+4m+1<1−4m
4m
2+8m<0
4m(m+2)<0
Sprzeczność, bo m>0
m<0
2m<−1−
√1−4m<0
2m+1<−
√1−4m<0
4m
2+4m+1>1−4m
4m
2+8m>0
4m(m+2)>0 ⇔ m+2<0, bo m <0
stąd m<−2
25 mar 12:07
Aga1: 1−4m≥0
25 mar 12:11
klo: dziękuję bardzo

25 mar 12:12
Aga1: Chyba nie jest dobrze, bo dla m=−1
?
25 mar 12:20
Godzio:
Ale mącicie !

Żeby 1 była między pierwiastkami to wystarczy warunek:
Δ > 0
f(1) * a < 1
25 mar 12:22
klo: czyli jet wszystko źle?
25 mar 12:24
Godzio:
f(1) * a < 0 oczywiście, raczej nie źle, jeśli było bezbłędnie robione, ale to kupa roboty

25 mar 12:25
klo: a z Twoich obliczeń Godzio jaki jest wynik?
25 mar 12:26
Godzio:
mx
2+x+1=0
Δ > 0
f(1) * a = (m + 2) * m < 0 ⇒ m ∊ (−2,0)
Odp: m ∊ (−2,0)
25 mar 12:26
25 mar 12:28
klo: czyli masz inny wynik
25 mar 12:29
Alkain: Godzio dlaczego tak jest z tym f(1)*a<1 ?
25 mar 12:30
Godzio:
No, najwidoczniej, jednak jestem pewien poprawności, narysuj sobie rysunek dla a > 0 i a < 0
(taki ogólny) i zobacz jakie warunki muszą być spełnione, żeby mieć pewność, że 1 nie wyskoczy
nam z przedziału pierwiastków,
a > 0 mamy, że f(1) < 0 (musi)
a < 0 mamy, że f(1) > 0, zatem widać, że iloczyn MUSI być ujemny:
a * f(1) < 0 w każdym przypadku
25 mar 12:31
Alkain: Ok już zrozumiałem trzeba przyznać, że cwany sposób

25 mar 12:34
Godzio: Jeżeli mamy do czynienia, z zadaniami typu
"Pierwiastki leżą między jakąś liczbą", "Oba pierwiastki są większe od jakieś liczby" itd.
To nigdy nie mamy tu wzorów Viete'a a już na pewno nie chodzi o wyznaczanie postaci
pierwiastków z delty itd. Tutaj działają właśnie takie zależności, wartość w liczbach jakie
mamy w poleceniu (w tym wypadku 1), w wierzchołku (czasem trzeba dać warunek dla wierzchołka)
no i dla współczynnika przy najwyższej potędze

25 mar 12:36
Aga1: Trening czyni mistrza.
Jak się nie ćwiczy to się zapomina, jedynie zostają w głowie wiadomości najczęściej używane.
Szybki sposób.
25 mar 12:41
MQ: Dzięki
Godzio 
−− no to czegoś się jeszcze nauczyłem
25 mar 12:45
Godzio:

25 mar 12:56
pigor: ...

no to może jeszcze dopowiem, że warunek
a*f(1)<0 ⇔ (a< 0 i f(1) >0)
lub (a >0 i f(1)< 0 , czyli "załatwia" nam
rozpatrywanie obu przypadków położenia paraboli (ramiona do dołu lub do góry),
a więc skraca robotę

. ...

25 mar 13:18
pigor: .. no i jeszcze warto (tym razem) pochwalić autora(ów) zadania którzy w ewidentny sposób ...

"podpowiedzieli" ... myślącemu uczniowi , że łatwe
policzenie f(1) może się ...

przydać w drugim problemie

. ...
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
tak powinno się układać zadania − moim − zdaniem , niech ten uczeń wie, że autor zadania
nie chce go ..."udupić" , ale dyskretnie pomóc w dojściu do rozwiązania . ...

25 mar 13:27
marti: x+1=1 i x+2=2
1 kwi 08:50

 za pomoc
za pomoc

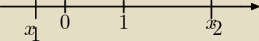 1∊(x1,x2)
x1<1
x2>1/*(−1)
x1<1
−x2<−1
−−−−−−−−−−−
x1−x2<0/*(−1)
x2−x1>0 /2
(x2−x1)2>0
(x12+x22)−2x1x2>0
(x1+x2)2−4x1x2>0
1∊(x1,x2)
x1<1
x2>1/*(−1)
x1<1
−x2<−1
−−−−−−−−−−−
x1−x2<0/*(−1)
x2−x1>0 /2
(x2−x1)2>0
(x12+x22)−2x1x2>0
(x1+x2)2−4x1x2>0


 Żeby 1 była między pierwiastkami to wystarczy warunek:
Δ > 0
f(1) * a < 1
Żeby 1 była między pierwiastkami to wystarczy warunek:
Δ > 0
f(1) * a < 1



 −− no to czegoś się jeszcze nauczyłem
−− no to czegoś się jeszcze nauczyłem

 no to może jeszcze dopowiem, że warunek
a*f(1)<0 ⇔ (a< 0 i f(1) >0) lub (a >0 i f(1)< 0 , czyli "załatwia" nam
rozpatrywanie obu przypadków położenia paraboli (ramiona do dołu lub do góry),
a więc skraca robotę
no to może jeszcze dopowiem, że warunek
a*f(1)<0 ⇔ (a< 0 i f(1) >0) lub (a >0 i f(1)< 0 , czyli "załatwia" nam
rozpatrywanie obu przypadków położenia paraboli (ramiona do dołu lub do góry),
a więc skraca robotę  . ...
. ... 
 "podpowiedzieli" ... myślącemu uczniowi , że łatwe policzenie f(1) może się ...
"podpowiedzieli" ... myślącemu uczniowi , że łatwe policzenie f(1) może się ...  przydać w drugim problemie
przydać w drugim problemie  . ...
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
tak powinno się układać zadania − moim − zdaniem , niech ten uczeń wie, że autor zadania
nie chce go ..."udupić" , ale dyskretnie pomóc w dojściu do rozwiązania . ...
. ...
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
tak powinno się układać zadania − moim − zdaniem , niech ten uczeń wie, że autor zadania
nie chce go ..."udupić" , ale dyskretnie pomóc w dojściu do rozwiązania . ...