rownanie prostej t@mi: dany jest trojkat ABC. A=(−2,−2) B=(2,4) C=(6,−4). a) wyznacz rownanie prostej, w ktorej zawarta jest wysokosc tego trojkata poprowadzona z wierzcholka A. b) Wyznacz dlugosc wysokosci trojkata poprowadzonej z wierzcholka A. c) wyznacz wspolrzedne takiego pkt. P ze punkt A jest srodkiem odcinka BP.

tim: Podp a) Wyznacz równanie prostej przechodzącej przez BC, a potem prostopadłą do niej przechodzącą przez A. b) Wyznaczasz punkt przecięcia się prostych BC oraz AH. Obliczasz odległość od tego punktu do punktu A.

t@mi: y=1/3x−4/3 a jak wyznaczyc prostopadla do niej przechodzaca przez A

tim: Jaki warunek muszą spełniać prostopadłe proste?

tim: Ale ta twoja funkcja nie przechodzi przez B oraz C.

t@mi: a1*a2=−1 musza spelniac ta zaleznosc

tim: Więc tak. Prosta |BC| y = − 2x + 8 Prosta |AH| prostopadła do |BC| musi mieć:"

	1
y =		x + z
	2

Podstawiamy punkt A. −2 = −1 + z z = −1 Wzór ogólny prostej:

	1
y =		x − 1
	2

b) Musimy znaleźć punkt przecięcia się prostych. Układamy układ równań z dwiema prostymi. {y = −2x + 8

	1
{y =		x − 1
	2

Rozwiązujemy wychodzi wynik.

Basia:

	1
czyli		*a2 = −1 ⇒ a2 = −3
	3

czyli pr.AA₁: y = −3x + b współrzędne punktu A(−2,−2) muszą spełniać to równanie czyli za x podstaw −2, za y też −2 i wylicz b A₁ to spodek wysokości wyprowadzonej z A na bok BC

tim: Basiu, tylko jego funkcja była zła..

Basia: Aaaaaaaaaaa czyli równanie pr.BC nie było poprawne. Założyłam, że jest. Działaj dalej Tim.

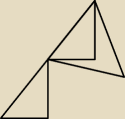
tim: c) Ja bym zrobił tak jako gimnazjalista. Wtedy tam byłby P.

Basia: Wskazówka: Jeżeli S jest środkiem odcinka o końcach M(x₁,y₁) i N(x₂, y₂) to

	x1+x2
xs =
	2

	y1+y2
ys =
	2

t@mi: dobra mniejwsza z wszystkim rownanie bc y=−2x=8 a prostopadlej do niej to y=1/2x−1. mam wszystko p[rocz policzonej wysokosci poprowadzonej z wierzcholka A. bo niewiem jak obliczyc jej dlugosc

Basia: a masz już współrzędne punktu przecięcia BC i wysokości AA₁ ? |AA₁| = √(x_a1 − x_a)² + (y_a1−y_a)²

t@mi: wlasnie nie wiem jak to liczyc, nie wiem jak obliczyc wspolrzedne pkt na ktory pada wysokosc opuszczona z wierzcholka A

tim: Podanym układem równań.

olaf: 1/ sposób ( najprościej) Długość wysokości to odległość p−tu A od prostej BC znasz wzór na odległość , więc już dasz radę obliczyć długość h 2/ sposób rozwiążac układ równań prostej BC i tej wysokości wyliczysz punkt przecięcia ( jest to spodek tej wys. policz odległość między A i tym spodkiem pozdro xD

t@mi: i o to mi chodzilo. bardzo dziekuje