kolokwium
analiza: Kolokwium analiza 2 moglby ktos spr.czy dobrze robie zad?
24 mar 14:47
analiza: 1.rozwiaz całki oznaczone,podaj interpretacje geometryczna wykonujac malunek
π 2π 2π
∫ sin2xdx=∫ sint= lim [cost] =[cos2π−cos0]=1−1=0
0 0 t−>∞ 0
t=2x
24 mar 14:51
analiza: oczywsicie zapomnialam o 1/2 bo 2xdx=dt czyli dx=dt/2
24 mar 14:52
analiza: Ale i tak wyjdzie 0?
24 mar 14:53
analiza:
3
∫x(x−2)dx moge podzielic na całke z x
2 i 2x

1
24 mar 15:02
pomagacz:
tak

24 mar 15:08
analiza: A ta piewsza cąłka ok?
24 mar 15:09
analiza: Mam zad wyznaczyc srednia wartosc funkcji f(x)=arctgx [0,
√3]
mam obliczyc
√3
0
24 mar 15:13
pomagacz:
tak, nawet nie musiałeś zmieniać granicy na 2π
| | ⎧ | t = 2x | |
| 0∫πsin(2x)dx = | ⎨ | dt = 2dx | =
|
| | ⎩ | dx = dt2 | |
| | 1 | | 1 | | 1 | |
= |
| 0∫πsin(t)dt = |
| [cos(2x)]0|π = |
| [cos(2π) − cos(0)] = 0 |
| | 2 | | 2 | | 2 | |
24 mar 15:14
24 mar 15:15
analiza: oblicz pole ograniczone krzywymi sin2x i sinx
24 mar 15:25
analiza:
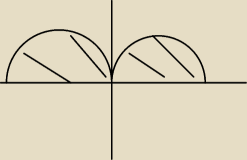
24 mar 15:27
analiza: czyli całka
π
∫
0
24 mar 15:27
analiza: zły rysunek

24 mar 15:28
analiza:
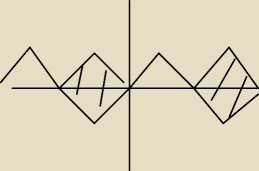
24 mar 15:30
analiza: O to pole chodzi?
24 mar 15:30
analiza: Cyzli np od 2pi do pi?
24 mar 15:31
pomagacz:
masz podany zakres do jakiego masz to pole policzyć?
f(x) = sin2(x)
g(x) = sin(x)
P = a∫b [f(x) − g(x)]dx = [F(x) − G(x)] a|b
24 mar 15:36
24 mar 15:39
pomagacz:
−π∫π [sin2(x) − sin(x)]dx
24 mar 15:39
analiza: Nie rozumiem czemu od −pi do pi
24 mar 15:41
analiza: przeciez te pole jest np od −pi do 0 lub od pi do 2pi
24 mar 15:42
analiza: Mam obliczyc pole jednego obszaru ograniczonego tymi krzywimi przepraszam z amale
niedoprecyzowanie
24 mar 15:43
pomagacz:
od [−π, 0] jest duże pole
od [0, π] jest takie malutkie pole, jak chcesz, możesz zsumować całeczki:
−π∫0[sin2(x) − sin(x)]dx + 0∫π[sin2(x) − sin(x)]dx = ...
24 mar 15:44
pomagacz:
zrób copyright tych krzywych w zeszyciku i zarysuj pole między nimi, tak łatwiej zawsze
zrozumieć o jakie pola chodzi

24 mar 15:45
analiza:
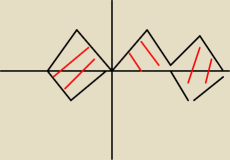
a juz czaje fakt chodzi o te pola
24 mar 15:47
24 mar 15:47
analiza: Dziekuje CI bardzo juz rozumiem
24 mar 16:03
analiza: Długosc krzywej y=√1−x2 x[0,1/2]
24 mar 16:10
analiza: 1/2
∫ √1+1/2(1−x2)2x
0
24 mar 16:11
analiza: czyli √1+(x−x2)2
24 mar 16:11
analiza: o boze zle pochodna

24 mar 16:13
 1
1





 a juz czaje fakt chodzi o te pola
a juz czaje fakt chodzi o te pola
