Planimetria Marta: Punkty A, B, C są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej AB, a punkty A, B, M wierzchołkami trójkąta równobocznego. Oblicz iloczyn sinusów kątów ostrych trójkąta ABC wiedząc, że pole tego trójkąta jest pięć razy mniejsze niż pole trójkąta ABM. Proszę o pomoc, bądź jakieś wskazówki.

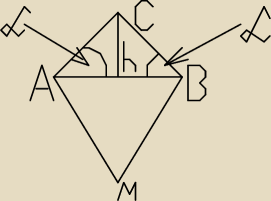
Coma13: P_AMB = a²√3/4 − taki wzór sinα=h/a/2=2h/a → h=asinα/2 P_AMB = 5P_ABC = 5 * a * h/2 = 5(a*asinα/2)/2 = 5a²sinα/4 5a²sinα/4 = a²√3/4 //*5 → 5a²sinα = a²√3 // :a² → 5sinα=2√3 → sinα=2√3/5 sin90^o=1 − sinus kąta prostego iloczyn sinusów = x = sin²α*sin90^o = 4*3/25 = 12/25

Bogdan: |BC| = a, |AC| = b, |AB| = |AM| = |BM| = c P_ABC = ¹₂ab, P_ABM = ¹₄c²√3 α = |<CBA|, 90^o − α = |<ABC| Mamy wyznaczyć:

	a		b		ab
sinα * sin(90o − α) = sinα * cosα =		*		=
	c		c		c2

c2√3		5ab
	=
4		2

	2
mnożymy obustronnie przez
	5c2

ab		√3
	=
c2		10

	√3
Odp.: sinα * sin(90o − α) =
	10

Coma13: przeczytałem: "trójkąta równoramiennego o przeciwprostokątnej" i to co narysowałem jest niemożliwe...no ale przemilczmy to...(chociaż może na globusie?)

Marta: Dziękuje serdecznie za pomoc!

Dominika: Punkty B,C są wierzchołkami trójkąta prostokątnego ABC. Bok BC jest najdłuższym z boków tego trójkąta, dwa krótsze są równoległe do osi układu współrzędnych. POMOCYY! potrzebuje na dzisiaj .