Dla "tęgogłowych" - Geometria
Coma13:
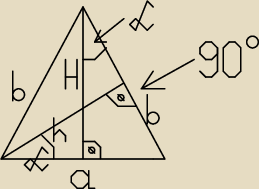
Trójkąt równoramienny ABC...
Wykaż, ze jeżeli a
2= H*h, to sinα=
√2 −1
12 kwi 18:07
Coma13:
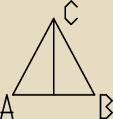
zapraszam do dyskusji... wiem że nie jest to trudne zadanie tylko trzeba wpaść na jakiś
plan...
12 kwi 18:53
Basia: Zapisz pole na dwa sposoby. Raz z h, raz z H.
Ale te kąty, które zaznaczyłeś nie muszą być równe (chyba, że to jest zadane z góry)
12 kwi 18:55
Mickej : to nie jest geometria to raz bo to jest figura płaska czyli chyba planimetria o ile sie
nie myle co mogło być dziwne aby trójkąt równoramienny był figurą przestrzenną a do
rozwiązania wykorzystaj podobieństwo trójkątów
12 kwi 18:57
Coma13: jak to α nie są równe

ale to są chyba dwa trójkąty prostokątne i mają wspólny kąt przy
wierzchołku B...... tzn do tego doszedłem z moją klasą na lekcji...tylko nam dzwonek
zadzwonił
12 kwi 18:59
Coma13: dobra planimetria.... ale czy te α które zaznaczyłem to na prawdę nie muszą być równe?
12 kwi 19:01
Coma13: tzn to jest geometria... bo Ziemia była kiedyś płaska (tzn zanim odkryto ze jest okrągła)

12 kwi 19:04
Coma13: bh/2 = aH/2 v
sinα=a/2b v
tgα=a/2h v
cosα=h/a
→ ctgαa2=a2/tgα → 1=1
12 kwi 19:12
Coma13: czy ja już mówiłem ze jakbym nie pisał dostaje tożsamość..? po prostu zaczynam wątpić
12 kwi 19:13
Bogdan:
Dobry wieczór.
Założenie: α € (0, 12π)
a2 = Hh => ha = aH
ha = cosα => aH = cosα => a/2H/2 = cosα => a/2H =
12cosα
tgα = 12cosα => sinαcosα = 12cosα => 2sinα = cos2α
sin2α + 2sinα − 1 = 0, Δ = 2√2
sinα = −√2 − 1 nie spełnia warunków zadania
lub
sinα = √2 − 1
12 kwi 19:18
Bogdan:
Rozjechało się, powtarzam tę sekwencję zapisów:
ha = cosα => aH = cosα => a/2H/2 = cosα =>
=> a/2H = 12cosα
12 kwi 19:22
Coma13: dziękuję, bardzo dobry...
a skąp wiedziałeś że "nagle trzeba użyć tangensa i zrobić tgα = 1/2 *cosα

hmmm

12 kwi 19:24
Coma13: tzn wszystko jest do odczytania...mimo tego że te ułamki taki malutkie się robią...
12 kwi 19:25
Bogdan:
Dobre pytanie − skąd wiadomo, że trzeba wybrać tę, a nie inną drogę?
To intuicja podparta doświadczeniem (wieloletnim).
Jeśli widzę iloczyn ab = cd, to zapisuję go w postacji proporcji: ac = db
lub ad = cb i sprawdzam, czy gdzieś w zadaniu jedna ze stron takiej proporcji
występuje.
Tu była właśnie taka sytuacja: aa = Hh
12 kwi 19:33
Coma13: ilu letnim? (to takie tylko niedyskretne pytanie)

ale bardzo dziękuje...
widzę że brakuje mi stażu w branży
12 kwi 19:37
Bogdan:
Wszystko przed Tobą. Zdobywanie doświadczenia (polegającego m.in. na codziennym
rozwiązywaniu zadań) w tej branży to duża przyjemność.

12 kwi 19:45
Coma13: zauważyłem, że to przyjemne...a na dodatek na forum nie bawię się sam...
matematykiem może nie będę ale jakiś poziom wypadałoby reprezentować
12 kwi 19:48
Bogdan:
Dobrze, że użyłeś słowa "zabawa", bo tak właśnie trzeba traktować matematykę.
To zabawa, rozrywka, ćwiczenia dla umysłu, a przy tym właśnie przyjemność dla całej
swojej osobowości, a nie, jak większość uważa, jakaś męczarnia i katorga.
12 kwi 20:12
Coma13: nie ma nic przyjemniejszego niż czuć, że się rozwija...w końcu "królowa nauk"
12 kwi 20:18
 Trójkąt równoramienny ABC...
Wykaż, ze jeżeli a2= H*h, to sinα=√2 −1
Trójkąt równoramienny ABC...
Wykaż, ze jeżeli a2= H*h, to sinα=√2 −1
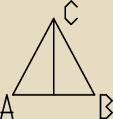 zapraszam do dyskusji... wiem że nie jest to trudne zadanie tylko trzeba wpaść na jakiś
plan...
zapraszam do dyskusji... wiem że nie jest to trudne zadanie tylko trzeba wpaść na jakiś
plan...
 ale to są chyba dwa trójkąty prostokątne i mają wspólny kąt przy
wierzchołku B...... tzn do tego doszedłem z moją klasą na lekcji...tylko nam dzwonek
zadzwonił
ale to są chyba dwa trójkąty prostokątne i mają wspólny kąt przy
wierzchołku B...... tzn do tego doszedłem z moją klasą na lekcji...tylko nam dzwonek
zadzwonił

 hmmm
hmmm
 ale bardzo dziękuje...
widzę że brakuje mi stażu w branży
ale bardzo dziękuje...
widzę że brakuje mi stażu w branży
