.
planimetria: Bardzo prosze o pomoc. W trapezie rownoramiennym ABCD podstawy maja dlugosc 32 i 24 a wysokosc
rowna 28. Oblicz promien okregu opisanego na tym trapezie.
22 mar 20:06
Dawid: Prowadzisz przekatna. Obliczasz z pitagorasa bok i to jest promien okregu opisanego na
trojkacie −przekatna trapezu bok trapezu podstawa trapezu
22 mar 20:35
planimetria: moglbys mi to narysowac?
22 mar 20:52
planimetria: ale skad wiem ze dluzsza podstawa przechodzi przez srodek okregu?
22 mar 20:56
Dawid: a dlaczego ma przechodzic?
22 mar 20:59
planimetria: no wtedy moge z pitagorasa skorzystac bo bede miala kat prosty,inaczej nie poprowadze
przekatnej tak zeby byl kat prosty
22 mar 21:00
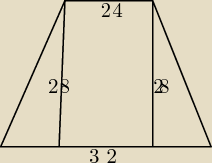
Dawid: Moj komputer jest tak stary że nie obsługuje rysunków ale zacznij od tego że nie musisz sie
przejmować okręgiem. Masz trapez rysujesz 2 wysokosci z wierzchołkow mniejszej podstawy.
dziela one dolna podstawe na 3 czesci, jedna rowna wiekszej a dwie czesci sa rowne i wynosza
liczysz z pitagorasa boki przekatna. A promien okregu bedzie tym samym promienem co okrag
opisany na trojkacie skladajacym sie z jednej podstawy boku i przekatnej
22 mar 21:04
planimetria: oj nie rozmumiem za bardzo tych dwoch ost linijek


22 mar 21:08
krystek:
22 mar 21:12
Eta:
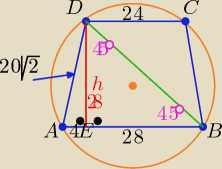
| | |AB|−|DC| | |
|AE|= |
| =........... = 4 |
| | 2 | |
to |EB|= 28
czyli ΔEBD jest prostokątny i równoramienny o kątach ostrych 45
0
Z tw. Pitagorasa wyznacz |AD|= .......... = 20
√2
| |AD| | |
| = 2R , R − dł. promienia okręgu opisanego na ΔABC |
| sin<(ABD) | |
zatem i jednocześnie na tym trapezie
R= .......... dokończ
22 mar 21:13
planimetria: Dziekuje Wam bardzo

**
22 mar 21:21




 **
**