Czworokąt Planimetria: Na boku AB trójkąta ABC wybieramy dowolnie punkt C1. Podobnie na boku BC wybieramy punkt A1,a na boku CA wybieramy punkt B1. Wykaż że okręgi opisane na trójkątach A₁B₁C, B₁C₁A i A₁C₁B przecinają sie w jednym punkcie. Co mam tu dokładniej wykazać , proszę o jakies wskazówki.

Hary:

Planimetria: nikt nie ma pomysłu ?

Planimetria: ,

Piotruś: Czy ktoś mógłby zrobić to zadanie?

Panko: Może kandydatem na ten punkt jest środek okręgu opisanego na ΔA₁B₁C₁ ? Zweryfikuj tę hipotezę .

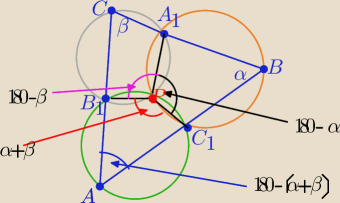
Eta: No to ... "widzę to tak" jak mawia pigor : ) okręgi o₁ i o₂ przecinają się w punkcie P okrąg o₁ jest opisany na czworokącie PA₁BC₁ to: miara kąta C _PA₁ = 180^o −α podobnie okrąg o₂ jest opisany na czworokącie B₁CA₁P to: miara kąta A₁PB₁= 180^o−β zatem miara kąta B₁PC₁= 360^o−(180^o−α+180^o−β)= α+β zaś miara kąta przy wierzchołku A trójkąta ABC jest też równa : 180^o−(α+β) zatem na czworokącie AC₁PB₁ też można opisać okrąg a okrąg ten jest jednocześnie opisany na trójkącie AC₁B₁ zatem okręgi opisane na trójkątach AC₁B₁ i BC₁A₁ i CA₁B₁ przecinają się w tym samym punkcie P co kończy dowód