Zadanie ze stereometrii
Cwiekk: Przeciwległe krawędzie boczne i przekątna podstawy ostrosłupa prawidłowego czworokątnego
tworzą trójkąt równoboczny o boku a. Oblicz sinus kąta nachylenia sciany do płaszczyznt
podstawy tego ostrosłupa.
Może mi ktos wytłumaczyć jak to obliczyć nie mając żadnych danych?
Wyjdzie sin60 − 0.8660?
12 kwi 14:49
Basia: Rozwiązuję
12 kwi 14:58
Cwiekk:
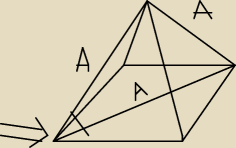
12 kwi 15:10
Basia:
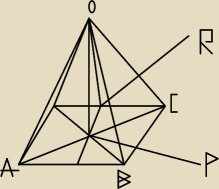
szukany kąt to kąt POR
AO = CO = AC = a
AB = BC = CD = AD = b
z tw.Pitagorasa
AC
2 = AB
2 + BC
2
a
2 = b
2 + b
2
2b
2 = a
2
PO jest wysokością tr.równobocznego AOC
| | PR | | a√2 | | 2 | | 2√2 | | √2 | |
sinα = |
| = |
| * |
| = |
| = |
| |
| | PO | | 4 | | a√3 | | 4√3 | | 2√3 | |
i to koniec rozwiązania bo w zadaniu pytają o sinα
samego α nie trzeba wyznaczać
12 kwi 15:11
Cwiekk: Dzięki bardzo
12 kwi 15:17
TommO: Mam te same zadanie, ale sie zastanawiam na tym czy policzyłaś sinus czy ctg.
Możesz jeszcze raz rzucić okiem?
13 kwi 17:48
TommO: Jak dla mnie powinno byc
sin = |PO| / |RO|
13 kwi 17:57
majkel: Basia ,chyba nie doczytała ,że chodzi o kąt między ścianą boczną a podstawą, a nie ścianą
boczną i wysokością. I chyba obliczyła ctg z tego co widzę na rysunku, ale za bardzo sie
nie znam. Niech ktoś bardziej ogarnięty sprawdzi.
13 kwi 18:15
Eta: Majkel masz rację, tak jest jak napisałeś!
Basia tego nie zauważyła

13 kwi 18:36
majkel: policzyłem ale chyba zamotałem,bo wyszedł mi sinus a√7
13 kwi 18:49
majkel: może ktoś sprawdzić czy dobrze?
13 kwi 19:03
Eta:
Nie liczyłam wcześniej

Teraz po policzeniu wychodzi mi ,że
sinα=
√427
bo H =
a√32
h
b=
a√144
sinα=
Hhb
sprawdź , czy się też nie rąbnęłam

13 kwi 19:04
majkel: nie wiem ,za kazdym razem wychodzi mi inny wynik
poza tym jesli ctg=
√6/6 = b/a
sin = a/c 6/c − ile c wynosi

Eta chyba masz źle
13 kwi 19:29
majkel: zrobilem to samo co Basia, wziąłem kąt miedzy H i Hb
13 kwi 19:32
Eta: A jednak mam dobrze

h
b2 = a
2 − (
a√24)
2
policz h
b i się przekonasz

ja przecież też liczyłam sinα=
Hhb
a Basia pomyłkowo wzięła
sinα=
b/2H −−−− tak przynajmniej widzę z Jej zapisu!
więc wynik nie może być taki!
13 kwi 19:58
Bogdan:
Dobry wieczór.
Już kilka razy tutaj omawialiśmy zależność w ostrosłupie prawidłowym n−kątnym
między miarą kąta α nachylenia ściany bocznej do płaszczyzny podstawy i miarą kąta β
nachylenia krawędzi bocznej do płaszczyzny podstawy ostrosłupa:
cosπn = tgβ*ctgα lub cosπn = ctgβ*tgα
W tym zadaniu:
n = 4,
β = 60o
Trzeba wyznaczyć sinα
13 kwi 20:29

 szukany kąt to kąt POR
AO = CO = AC = a
AB = BC = CD = AD = b
z tw.Pitagorasa
AC2 = AB2 + BC2
a2 = b2 + b2
2b2 = a2
szukany kąt to kąt POR
AO = CO = AC = a
AB = BC = CD = AD = b
z tw.Pitagorasa
AC2 = AB2 + BC2
a2 = b2 + b2
2b2 = a2

 Teraz po policzeniu wychodzi mi ,że
sinα= √427
bo H = a√32
hb= a√144
sinα= Hhb
sprawdź , czy się też nie rąbnęłam
Teraz po policzeniu wychodzi mi ,że
sinα= √427
bo H = a√32
hb= a√144
sinα= Hhb
sprawdź , czy się też nie rąbnęłam 
 Eta chyba masz źle
Eta chyba masz źle
 hb2 = a2 − (a√24)2
policz hb i się przekonasz
hb2 = a2 − (a√24)2
policz hb i się przekonasz ja przecież też liczyłam sinα=Hhb
a Basia pomyłkowo wzięła
sinα= b/2H −−−− tak przynajmniej widzę z Jej zapisu!
więc wynik nie może być taki!
ja przecież też liczyłam sinα=Hhb
a Basia pomyłkowo wzięła
sinα= b/2H −−−− tak przynajmniej widzę z Jej zapisu!
więc wynik nie może być taki!