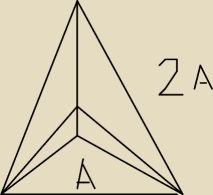
oblicz cosinus... Hub: W ostrosłupie prawidłowym trójkątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.

tim: Have you got an answer?

Hub: tak, tzn mam nawet schemat rozwiązania

Hub: ale nie wiem z czego wynikają poszczególne kroki

Hub: już go przedstawiam

Hub: wyznaczenie ściany bocznej ISMI w zależności od a. S to wierzchołek ostrosłupa a M to punt na krawędzi A do którego opuszczona jest wysokość ściany bocznej. SM ma być równe ^a√15₂

Hub: dalej wyznaczamy długość wysokości tej samej ściany bocznej, ale opuszczonej na krawędź 2A. i powinno wyjść IBEI= ^a√15₄

Hub: i teraz już z twierdzenia cosinusów wyznaczamy cosinus α. i cosα= ⁷₁₅

Hub: czy ktoś potrafi rozwiązać od początku do końca ?

Basia: Witaj! Spróbuję

Basia: ABC podstawa SM − wysokość jednej ściany bocznej SN − wysokość drugiej ściany bocznej AB = BC = AC = a SA = SB = SC = 2a SM = SN z tw.Pitagorasa SM² + AM² = AS²

	a
AM =
	2

	a2
SM2 +		= 4a2
	4

	a2		16a2 − a2		15a2
SM2 = 4a2 −		=		=
	4		4		4

	a√15
SM = SN =
	2

trójkąt NSA jest równoramienny szukany kąt to kąt NSA musimy obliczyć NM odcinek NM łączy środki boków tr.równobocznego o boku a czyli

	a
NM =
	2

i teraz stosujemy tw.cosinusów NM² = SN² + SM² − 2SN*SM*cosα

a2		15a2		15a2		a√15		a√15
	=		+		− 2*		*		*cosα /*4
4		4		4		2		2

a² = 15a² + 15a² − 30a²*cosα /:a² 1 = 30 − 30cosα 30cosα = 29

	29
cosα =
	30

Basia: Nie bardzo rozumiem po co chciałeś liczyć BE ?

Hub: gdzieś musi być mały błąd bo w odpowiedzi jest cosα = ⁷₁₅

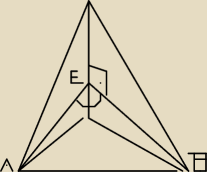
Hub: tzn chyba już rozumiem rozbieżność, to nie ten kąt. zgodnie z twierdzeniem cos. tutaj IABI²=IAEI²+IBEI²−2IAEIIBEI cos α

Hub:

Basia: Błąd może być w odpowiedzi. Tutaj naprawdę żadnego nie widzę. Sprawdź jeszcze raz czy dokładnie przepisałeś treść zadania.

Coma13: Sposób się liczy a nie wartość liczbowa

Basia: no dobrze

	a√15
mamy SM =
	2

	a*SM		a2√15
PASC =		=
	2		4

	2a*AE
PASC =		= a*AE
	2

	a2√15
a*AE =
	4

	a√15
AE =
	4

	a√15
BE = AE =
	4

AB=a z tr.AEB

	15a2		15a2		15a2
a2 =		+		− 2*		*cosα /*16 : a2
	16		16		16

16 = 30 − 30cosα 30cosα = 14

	14		7
cosα =		=
	30		15

z katami dwuściennymi zawsze byłam "na bakier" faktycznie kąt o który chodzi to kąt AEB