funkcja lil: Pomoże mi ktoś z tymi zad, bo nie mam pojęcia o co w nich chodzi. Wyznacz wzór funkcji liniowej, wiedząc, że 1. f(−4)=−12, f(x)<0⇔x∊(−∞,2). 2. f(√2)=2 ∧ x∊R(nad tym jest taki daszek), f(x)>0.

Artur z miasta Neptuna: funkcja liniowa ma postać: y =ax+b f(−4)=−12 ... oznacza, że: −12 = a*(−4) + b f(x)<0⇔x∊(−∞,2) ... oznacza, że rozwiązanie nierówności: ax+b<0 jest x∊(−∞,2), a także (w przypadku funkcji liniowych) a*(2) + b = 0 masz dwa równania ... wylicz 'a' i 'b'

Aga1: 1. Miejscem zerowym jest 2 tzn. ,że punkt (2,0) należy do wykresu oraz (−4,−12)należy do wykresu. Wzór funkcji liniowej y=ax+b Oblicz a oraz b z układu równań 2a+b=0 −4a+b=−12 2. podobnie.

lil: Wyszło mi, że a=2 a b=−4. Czyli wzór funkcji to y=2x−4?

Artur z miasta Neptuna: tak

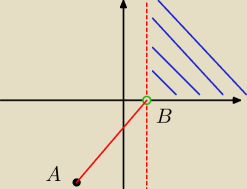
asdf: f(−4) = −12 <<<<<<<< czytam: dla argumentu równego −4, funkcja ma wartość −12, czyli: dla x = −4 y = 12 A = (−4; −12) f(x)<0 w przedziale (−∞;2) funkcja jest mniejsza od 0 w przedziale od − nieskonczonosci do 2, więc 2 jest miejscem zerowym funkcji. f(0) = 2, czyli dla argumentu równego 2, funkcja ma wartość 0 B = (2;0) −−−−−−−−−−−−−−−−−−−−−−−−−−− y = ax + b podstawiam punkt A: −12 = −4a + b teraz B: 0 = 2a + b klamra: −12 = − 4a + b 0 = 2a + b /klamra odejmuje i jest: −12 = −6a a = 2 −−−−−−−−−−−−−−−−− 0 = 2*2 + b b = −4 −−−−−−−−−−−−−−−−−− y = 2x − 4

lil: Dziękuję bardzo wszystkim za pomoc. Teraz już rozumiem jak robić podobne zad