Przedzialy monotonicznosci i ekstrema lokalne funkcji Raptiles: Mam problem z rozwiazaniem kilku zadan. 1. f(x) = x⁴ − 3/4 x ³ +3 Licze najpierw pochodna z tego i wychodzi mi tyle x²(4x−4) Co dalej? 2 fukcje z tego sa? 2. f(x) = (x² − 1)e^x tego przykaldu z liczba e juz kompletnie nie rozumiem 3. f(x) = x/x² + 4 (x² + 4 w mianowniku)

Artur z miasta Neptuna: 1.

	3
a od kiedy		* 3 = 4
	4

2. (fg)' = f'g + fg' f = x²−1 g = e^x 3.

x
x2−4

	f		f'g − fg'
(		)' =
	g		g2

Artur z miasta Neptuna: co później To: https://matematykaszkolna.pl/strona/381.html https://matematykaszkolna.pl/strona/387.html

Raptiles: Sorry w zadaniu jest 4/3 x po skroceniu i wyciagnieciu x² przed nawias mam wartosc x²(4x−4) w innym zadaniu bylo latwiej bo wyznaczalem Δ oraz X1 i X2. Odrazu wiedzialem przedzialy monotonicznosci i ekstrema. A tutaj x² = 0 to parabola a 4x−4 to prosta.

Raptiles: Dobra 1 zrobilem

Artur z miasta Neptuna: x²(4x−4) = 4x²(x−1) czyli masz dwa miejsca zerowe: 0, 1 gdzie: 0 −−− podwójne (parzyste) miejsce zerowe 1 −−− pojedyncze (nieparzyste) miejsce zerowe wiesz jak się szkicuje wykres wielomianów stopnia 'n' posiadający miejsca zerowe parzyste/nieparzyste ?

Raptiles: Nie mialem stycznosci z miejscami parzystymi i nieparzystymi. Wyszlo mi ze funkcja f(x)' > 0 dla x ∊ (1,∞) a mniejsza od zera dla x ∊ (−∞, 1) Minimum lokalne to 1 i 8/3

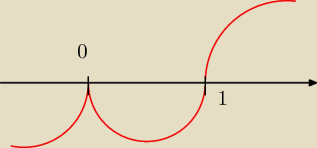
Artur z miasta Neptuna: i źle masz, bo f(x) jest malejąca dla (−∞,0) oraz w (0,1) ... uwaga nie sumuj tych przedziałów ... wypisuje się je po przecinku jako: w (,), w (,), w (,)

Raptiles: Dzięki za pomoc

Aga1: Właśnie, kiedyś na tym forum napisałam, że przy monotoniczności na ogół przedziałów nie łączy się sumą . Ktoś napisał " nie słuchaj jej". Odpisałam, że "nie chcę polemizować", i był jeszcze jeden niewybredny wpis. Wtedy nikt mnie nie poparł.

Aga1: Właśnie, kiedyś na tym forum napisałam, że przy monotoniczności na ogół przedziałów nie łączy się sumą . Ktoś napisał " nie słuchaj jej". Odpisałam, że "nie chcę polemizować", i był jeszcze jeden niewybredny wpis. Wtedy nikt mnie nie poparł.

Raptiles: Mam problem tylko z ta liczba e. Pochodna funkcji wyszła mi: 2xe^x + x²e^x − e^x jak mam porównać to do zera i wyznaczyć miejsca zerowe?

Artur z miasta Neptuna: e^x przed nawias a następnie: ∀_x∊Df e^x > 0 ... więc zajmujesz się tylko tym co w nawiasie

Artur z miasta Neptuna: Aga1 −−− nie wiem kiedy to było ... może wtedy mnie jeszcze nie było tutaj

Aga1: Rozwiązuję zadania kilka miesięcy,trudno mi jest umieścić w czasie.

Raptiles: Wyszła mi funkcja (2x + x² − 1 ) minimum to −1+√2 a max to −1−√2 F maleje między tymi przedziałami a rosnie (−∞ −1−√2) u (−1+√2 ∞) dobrze zrobiłem

Artur z miasta Neptuna: BEZ SUMY patrz co pisałem o 11:33

Artur z miasta Neptuna: przedziały piszesz po przecinku

Raptiles: Dobra już zapamiętałem

Artur z miasta Neptuna: dobra rada:

	f
... jeżeli masz obliczyć pochodną postaci:		... to po obliczeniu pochodnej nigdy (ale to
	g

nigdy) nie skracaj czegokolwiek z mianownikiem ... niech w mianowniku zawsze będzie parzysta potęga dlaczego? bo wtedy ∀_x∊Df mianownik pochodnej > 0 ... więc interesuje Ciebie tylko znak licznika

Raptiles: Zostało mi tylko 1 zadanie. Ekstrema globalne, wyznaczyć najmniejsze i największe wartości funkcji f(x) = x−1/x+1 <0,4> Łatwiejsze przykłady typu x² − 2x + 3 zrobiłem bez problemu bo łatwo się podstawiało. Ale tutaj mam problem

Artur z miasta Neptuna: zasada zawsze jest taka sama: 1) sprawdzasz czy w danym przedziale funkcja jest ciągła 2) wyliczasz wartość f(x) na krańcach badanego przedziału 3) obliczasz pochodną 4) wyznaczasz ekstrema (f'(x) = 0) 5) jeżeli jakieś ekstremum jest w badanym przedziel to obliczasz wartość funkcji dla tego punktu 6) porównujesz wartości tych punktów i wybierasz największe i najmniejsze wartości

Artur z miasta Neptuna:

x−1		x+1 − 2		2
	=		= 1 −
x+1		x+1		x+1

teraz łatwiej będzie

Raptiles: Nawet nie wiem jak ty to zrobiłeś...

Raptiles: Dobra juz wiem

Artur z miasta Neptuna: x−1 = x +1 − 2 ... prawda ... = (x+1) − 2

Raptiles: Ale nic mi nie mówi takie przekształcenie