monika: Długości boków trójkąta prostokątnego tworzą ciąg geometryczny. Oblicz iloraz tego ciągu. Wiem, że trzeba jakoś zacząć, że a²+b²=c² a₁²+(a₁q)²=(a₁q²)² ale to jest jedno równanie i dwie niewiadome. Nie wiem jak ułożyć drugie do układu równań.

monika: Podnoszę zadanie. Może jednak ktoś chciałby pomóc.

monika: Nikt nie wie...

monika: Up, up

Kona: Z.: a₁>0, q>1 a₁²+(a₁q)²=(a₁q²)² a₁²+a₁²*q²=a₁²*q⁴ ∥:a₁² 1+q²=q⁴ Oznaczmy z=q² (z jest >1), a więc q=√z (tylko liczba dodatnia − patrz założenie) 1+z=z² Stąd −z²+z+1=0 (równanie kw.) Δ=5 , z₁=1+√5 (akceptujemy, bo >1) , z₂=1−√5 (liczba ujemna − odrzucamy) q=√z A więc ostatecznie q=√1+√5

Kora: poprawka z1=1+√5\2 (akceptujemy, bo >1) , z2=1−√5\2 (liczba ujemna − odrzucamy) wynik q=√(1+√5)\2

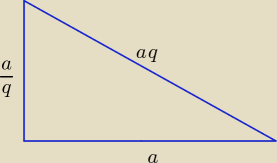
Bogdan: a > 0

a2		q2
	+ a2 = a2q2 / *		⇒ q4 − q2 − 1 = 0,
q2		a2

	1 − √5
Δ = 5, q2 =		< 0 sprzeczność
	2

	1 + √5
lub q2 =		⇒ q = ...
	2

Saizou : wariant 1 gdy x>0 q>1 x²+x²q²=x²q⁴ x²+x²q²−x²q⁴=0 x²(1+q²−q⁴)=0 q²=t x²(−t²+t+1)=0 −t²+t+1=0 Δ=1+4=5

	−1−√5		1+√5
t1=		=
	−2		2

	−1+√5		1−√5
t2=		=		sprzeczność
	−2		2

	1+√5
q2=
	2

	1+√5		1+√5
q=√		lub q=−√		sprzeczność
	2		2

wariant 2 a>0 −1<q<1 x²q⁴+x²q²=x² x²q⁴+x²q²−x²=0 x²(q⁴+q²−1)=0 q²=t x²(t²+t−1)=0 t²+t−1=0 Δ=1+4=5

	−1−√5
t1=		sprzeczność
	2

	−1+√5
t2=
	2

	−1+√5
q2=
	2

	−1+√5		−1+√5
q=√		lub q=−√		sprzeczność
	2		2

ostatecznie

	−1+√5		1+√5
q=√		lub √
	2		2

Jeśli czegoś nie pomyliłem