| 3√3 | ||
Oblicz dlugość krótszej przekątnej sześciokąta foremnego o polu | ||
| 2 |
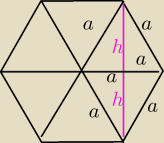 pole =6*pole trójkata równobocznego
pole =6*pole trójkata równobocznego
| 3√3 | a*h | ||
=6* | |||
| 2 | 2 |
| 3√3 | |
=h | |
| 6a |
| a√3 | 2h | |||
h= | ⇒a= | |||
| 2 | √3 |
| 3√3*√3 | |
=h /*h | |
| 6*2h |
| 9 | |
=h2 | |
| 12 |
| 3 | 3 | |||
h= | = | |||
| √12 | 2√3 |
| 6 | ||
d=2*h= | = | |
| 2√3 |
 Nie wiem czy dobrze, bardzo proszę o sprawdzenie i ewentualne poprawienie !
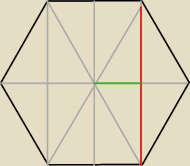
W każdym sześciokącie foremnym mieści się 12 jednakowych trójkątów 30−60−90 ( jak na rysunku)
Nie wiem czy dobrze, bardzo proszę o sprawdzenie i ewentualne poprawienie !
W każdym sześciokącie foremnym mieści się 12 jednakowych trójkątów 30−60−90 ( jak na rysunku)
| a2√3 | 3√3 | |||
Tak więc mamy zależność 12* | = | , gdzie a to krótsza przyprostokątna w | ||
| 4 | 2 |
| 3√3 | ||
3a2√3 = | ||
| 2 |
| 3 | ||
3a2 = | ||
| 2 |
| √2 | ||
a= | ||
| 2 |
| √2 | ||
(kolor czerwony na rys.). więc mamy działanie 2(a√3)= 2( | *√3) =√6 | |
| 2 |

| 6 | 3√3 | |||
u mnie d= | = | =√3 | ||
| 2√3 | 3 |
