Planimetria! euklides: Planimetria! Oblicz pole P pierścienia kołowego ograniczonego okręgiem wpisanym w trójkąt ABC i okręgiem opisanym na nim, gdy: a=(−5,5) b=(5,−5) c=(5,5)

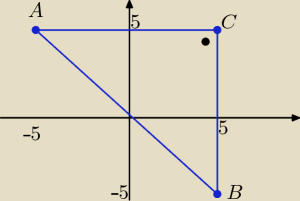
Eta: Trójkąt ABC jest prostokątny i równoramienny ( połowa kwadratu o boku dł 10 a=b=|AC|=|BC|=10 c=|AB|= 10√2

	c		a+b−c		10+10−10√2
R(op) =		= 5√2 rw =		=		= 10−5√2
	2		2		2

P(pierścienia)= πR²− πr²=............. dokończ

aaa: 50π−π(100−100√2+50)=π(50−100+100√2−50)=π(100√2−100)=100(√2−1)*π