Wyznacz pozostałe funkcje trygonometryczne Michał:

	3
Wyznacz funkcje trygonometryczne kąta ostrego α, wiedząc że sin α =		.
	17

Tragos: sin²α + cos²α = 1 cos²α = 1 − sin²α (α − ostry) cosα = √1 − sin²α

	sinα
tgα =
	cosα

	1		cosα
ctgα =		=
	tgα		sinα

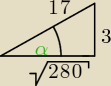
asdf: x² + 3² = 17² x² = 17² − 3² x² = 289 − 9 x = √280 x = 2√70 sin =... cos = ... tg = ... ctg = ...

Michał: Tak do tego już doszedłem, ale nie wiem co zrobić dalej bo wychodzi mi, że cosα = U{√280{17}

asdf: no i co w tym złego?

Michał: No właśnie nie wiedziałem co robić z √280

asdf: zostawić jak jest w mianowniku to można wyprowadzic, ale tak to już nic nie zrobisz

Tragos: zapisz w formie 2√70 i jest ok

asdf: tutaj masz przykład wyprowadzenia:

	3		3		2√70		6√70
tgα =		=		*		=
	2√70		2√70		2√70		280

Tragos:

	3√70
asdf to wypada jeszcze skrócić na
	140

asdf: masz racje

Michał: Teraz rozwiązuje wielomiany, ale nie wiem czy dobrze obliczyłem drugi x ? 2x³ − x² + 2x − 1 = 0 x²(2x − 1) + 1(2x*1) = 0 (2x − 1) (x² + 1) = 0 2x − 1 = 0 x² + 1 = 0 2x = 1 /:2 x² = −1

	1
x =		x = −1
	2

asdf: żadna liczba podniesiona do potęgi nie da ujemnej, sprawdź sobie to delta wyjdzie Ci ujemna

krystek: A oblicz ile to (−1)²=?

Michał: Oj no tak dzięki

asdf: 1?

Michał: Tak

Michał: 1.Rozłóż na czynniki liniowe wielomiany: W(x) = x3 + 3x2 − 4x − 12 W(x) = x3 + 4x2 − 2x − 8 2. Sprawdź, czy podana liczba jest pierwiastkiem wielomianu: a) W(x) = 3x3 + x2 − 6x − 2 gdzie x = 1 b) W(x) = 2x3 − 6x2 − 3x + 1 gdzie x = −2

Michał: Nie wiem jak dobrze to zrobić. Próbuję, ale nie wiem ! Pomocy