. Basiak: Pole czworokąta wypukłego jest równe 3, a przekątne tego czworokata mają długości 6 i 2. Oblicz miarę kąta, pod jakim przecinaja się te przekątne. k,l − przekątne czworokąta wypukłego α− kąt między przekątnymi Pole czworokąta:

	1
P=		kl sinα może mi ktos wytłumaczyć czemu taki wzór
	2

Saizou : witaj Basiek podbijam Twój post

cziki: P=3 P=¹₂sinα* ac +¹₂sin(180− α)ad + ¹₂ sinα db + ¹₂sin(180− α)bc 3=¹₂ sinα (ac+ ad + db + bc) 3=¹₂ sinα(a+b)(c+d) a+b=2 c+d= 6 3=¹₂ sinα 2*6 sinα= ¹₂ α=30

cziki: c

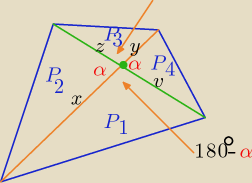Eta: x+y=k v+z=l P= P₁+P₂+P₃+P₄ sin(180^o−α)=sinα

	xv		xz		zy		vy
P1=		*sinα P2=		*sinα P3=		*sinα P4=		*sinα
	2		2		2		2

	sinα		sinα		1
P=		(xv+xz+zy+vy)=		(x+y)(v+z)=		k*l*sinα
	2		2		2