kolega tak mi rozwiązał, poproszę o sprawdzenie ostrosłup: Zadania W ostrosłupie prawidłowym sześciokątnym o wysokości 2√3 cm, ściana boczna jest nachylona do płaszczyzny podstawy pod kątem alfa=pi/3. Oblicz objętość i pole powierzchni bocznej ostrosłupa. Rozwiązanie dane: h=2√3 cm, kąt alfa=60 V=1/3Pp*h Pp=3a²√3/2 tg30=a/2√3 √3/3=a/2√3 //*2√3 a=6/3=2cm Pp=6√3cm² V=2√3cm*2√3cm²=12cm³ Pb=6*1/2ah₂ (h₂)²=b²−1 (h₂)²=a²+h²−1 (h₂)²=4+12−1 h₂=√15cm Pb=6√15cm²

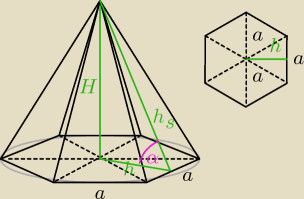
dero2005: H = 2√3 cm α = 60^o

H		√3
	= sin 60o =
hs		2

	2√3
hs =		H = 4 cm → wysokość ściany bocznej
	3

h = √h_s² − H² = √4² − (2√3)² = √16−12 = √4 = 2 cm

	2		4
a =		√3h =		√3 cm → krawędź podstawy
	3		3

	3a2√3
Pp =		= 8√3 cm2 → pole podstawy
	2

	4
Pb = 3*a*hs = 3*		√3*4 = 16√3 cm2 → pole boczne
	3

	Pp*H		8√3*2√3
V =		=		= 16 cm3 → objętość
	3		3

reksio: sorry ale objetosc jest 12cm³

dero2005: Dlaczego?

ostrosłup: Mam pytanie, czy nachylenie krawędzi ściany do podstawy również wynosi 60 stopni?

ostrosłup: i dziękuję za odpowiedź...

ostrosłup: bo wydaje mi się, że przy krawędzi ten kąt jest mniejszy i stąd ta róznica w wynikach

dero2005: W zadaniu napisałeś, że ściana boczna (nie krawędź ) jest nachylona do

	π
podstawy pod kątem		czyli 60o, natomiast krawędź boczna ostrosłupa jest nachylona do
	3

podstawy pod kątem ≈62^o34'

dero2005: poprawka − kąt pochylenia krawędzi bocznej wynosi ≈56^o19'