funkcja wykładnicza asdf:

	a
y =		+ 3
	x − 2

a)oblicz a b)dla jakich argumentów funkcja przyjmuje wartości > 1 c) m−ce zerowe funkcji −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Tak po krótce to mógłby ktoś mi powiedzieć na czym polega ta funkcja wykładnicza? Po internecie chodzic i słuchać tych definicji to nie idzie Proste zadanie a nie moge zrobić

Artur z miasta Neptuna:

	a
wykładnicza czyli		to hiperbola w ćwiartkach I i III (dla a>0) i w II i IV (dla a<0)
	x

dlatego już wiem, że a<0 w tym przypadku no i w sumie tyle by było poza wyglądem hiperboli (który znasz) nic więcej nie trzeba mówić, czego byś nie wiedział z poprzednich funkcji (np. jak przesuwać o wektor)

Aga1:

	a
y=		to funkcja wymierna, a wykładnicza to y=ax
	x

asdf: a to nie są ćwiartki 2 i 4?

Artur z miasta Neptuna: asdf −−− są i dlatego a<0

Artur z miasta Neptuna: Aga1 −−− fakt

asdf: coś nie podchodzi mi te zadanie później spróbuje rozwiązać jak poducze się troche teorii...dzięki

pigor: ... to nie jest funkcja wykładnicza , lecz wymierna (homograficzna) − wykres to hiperbola

	a
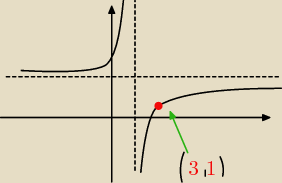
a) f(x)=		+3 ⇒ rozwiąż równanie f(3)=1 ⇒ a+3=1 ⇔ a= −2 ;
	x−2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	−2
b) f(x)>1 ⇔		+3>1 \ /*(x−2)2 i x≠2 ⇒ −2(x−2)+2(x−2)2 >0 ⇒
	x−2

−(x−2)(2+2x−4)>0 ⇔ −2(x−2)(x−1)>0 /:(−2) ⇔ (x−2)(x−1)<0 ⇔ x∊(2;2) −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	−2
c) f(x)=0 ⇔		+3=0 ⇒ −2+3(x−2)=0 i x≠2 ⇒ 3x=8 ⇔ x=83 . ...
	x−2

asdf: o kurde pigor to podobne w takim razie wszystko jest do f. kwadratowej.... funkcja wymierna to parabola podzielona względem swojej osi symetrii? w b nie powinno być x ∊ (2;1)?

Artur z miasta Neptuna: asdf −−− brrr ... żadna parabola ... to jest hiperbola

asdf: ale ja nie napisałem, że to jest parabola Dam sobie spokój z tym zadaniem jeżeli mam takie braki

pigor: ... tak powinno być (2,1), przepraszam . ... a Artur z ... ma rację , a ty nic na ... skróty, trochę hamuj , bo wielu na tej funkcji sobie pazurki ... łamie , pozdrawiam was obu

asdf: ja nawet nie mam zamiaru spisywać tego zadania do zeszytu Jak zrozumie to sam zrobie, dzięki