Liczba punktów wspolnych okregu
invisible: Liczba punktów wspolnych okregu o rownaniu (x−1)2+y2=4 z prosta o rownaniu y=−1 jest rowna?
20 mar 09:12
Artur z miasta Neptuna:
y=−1 ... wstawiasz do wzoru na okrąg i obliczasz ... podpowiem −−− 2 punkty wspólne
20 mar 09:17
Artur z miasta Neptuna:
a jeszcze prościej −−− rysujesz okrąg i tą prostą i widzisz ile razy się przecinają
20 mar 09:17
invisible: Nigdzie nie moge znalezc tego wzoru
20 mar 09:21
Artur z miasta Neptuna:
jakie wzoru
tutaj nie ma ŻADNEGO wzoru
tutaj masz podstawić y=−1 do (x−1)
2 + y
2 = 4 .... otrzymując (x−1)
2 + (−1)
2 = 4 ... i
wyliczyć 'x'
20 mar 09:22
konstruktorok.republika.pl: Podstaw do równania okręgu zamiast y −1, wówczas rozwiąż równanie ze względu na x. Trzeba
będzie policzyć miejsca zerowe. Mi wyszły 2 rozwiązania, tj 2 punkty wspólne.
20 mar 09:23
Aga1:
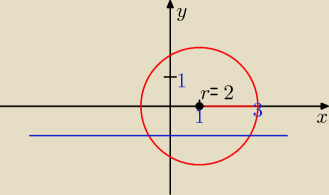
S(1,0)
20 mar 09:27
invisible: (x−1)
2=3
tak i teraz musze to (x−1)
2 obliczyc ze wzoru a
2−2ab+b
2?
20 mar 09:27
invisible: (x−1)
2=3
tak i teraz musze to (x−1)
2 obliczyc ze wzoru a
2−2ab+b
2?
20 mar 09:30
konstruktorok.republika.pl: Podstaw do równania okręgu zamiast y liczbę −1, wówczas rozwiąż równanie ze względu na x.
Trzeba
będzie policzyć miejsca zerowe. Mi wyszły 2 rozwiązania, tj 2 punkty wspólne.
Tj.
(x−1)2+y2=4
(x−1)2+(−1)2=4
20 mar 09:31
invisible: x=1 y=1 r=2
20 mar 09:33
Aga1: Nie trzeba liczyć x i y, bo jest pytanie ile
Więc po podstawieniu do równania okręgu zamiast y
otrzymujemy równanie kwadratowe, wystarczy obliczyć Δ
A jeśli rozwiązywać, to raczej bez Δ
(x−1)2=3
√(x−1)2=√3
Ix−1I=√3
x−1=√3 lub x−1=−√3
20 mar 09:40
invisible: ok dzieki
20 mar 09:42