Zadanie logiczne Marcin: Mamy pole o wielkości 6x6 oraz lafelki 3x1. Musi zostać jak najwięcej pustych pól.

Artur z miasta Neptuna: a jeszcze wyjaśnij −−− co mamy robić, aby kombinować z tymi pustymi miejscami

Marcin: Zadanie brzmi tak: Pewien student zaczął układać kafelki a że był strasznie zmęczony to nie układał tego dokładnie, w końcu nie miał już miejsca żeby je przyklejać. Nie można ich przycinać ani nakładać na siebie. Dowiedziałem się, że takich pustych miejsc może być 15 i trzeba uzasadnić czemu nie 16.

Artur z miasta Neptuna: po pierwsze 6x6 = 36 3x1 = 3 więc ilość wolnych miejsc = 36 − 3k ... gdzie k −−− ile student kafelek położył i wiesz, że 36 podzielne przez 3 oraz 3k podzielne przez 3 więc (36−3k) będzie podzielne przez 3 więc ilość wolnych miejsce ∊ {0,3,6,9,12,15,18,21,24,27,30,33,36}

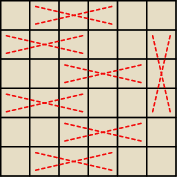
Artur z miasta Neptuna: przykładowe rozwiązanie

Artur z miasta Neptuna: więc jak już ... to musisz uzasadnić, dlaczego nie może być 18 wolnych miejsc

Marcin: Czyli jakie jest dokładne uzasadnienie, że nie może być 18 i więcej?

Artur z miasta Neptuna: uzasadnienie opisowe załóżmy, że jest 18 miejsc wolnych ... czyli połowa ... podzielny ten kwadrat 6x6 na 6 równych części po 1x6 każdy w każdej z tych części wkładamy jedną kafelkę, tak aby nie można było ułożyć już następnej kafelki (czyli jest __ X X X __ __ albo __ __ X X X __. Tylko w ten sposób w każdej części mamy 3 wolne miejsca co w sumie daje nam 18 wolnych miejsc Składamy te części w całość tworząc kwadrat 6x6 i okazuje się, że jest możliwość położenia dodatkowych kafelek w pionie. Czyli ilość wolnych miejsc <18.

Marcin: Ok, dzięki wielkie za pomoc