Wiedząc że tgx=2, oblicz wartość wyrażenia U{ sinx }{ cos^2x } Paulina:

	sinx
Wiedząc że tgx=2, oblicz wartość wyrażenia
	cos2x

cześć: bierzemy wzór: tgx= ^sinx_cosx czyli: 2=^sinx_cosx co daje nam 2cosx=sinx teraz z użyciem jedynki trygonometrycznej obliczamy wartość cosx sin²x+cos²x=1 (2cosx)²+cos²x=1 5cos²x=1 / :5 cos²x = ¹₅ cosx = ¹_√5 = ^√5₅ teraz obliczymy wartość sinx jesli 2cosx=sinx to ^2√5₅=sinx wystarczy teraz tylko podstawic dane do wyrażenia i koniec

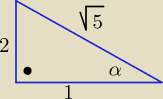
Eta: dla x€ (0^o,90^o)

	1
cosx=
	√5

	sinx		1
W=		= tgx*		=2*√5
	cos2x		cosx

Basia: nie czepiam się, ale w zadaniu nie jest napisane, że kąt jest ostry i wobec tego są dwa rozwiązania

	1		1
cosx =		lub cosx = −		itd.
	√5		√5

Eta: Oczywiście