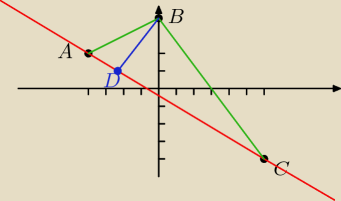
 Przy punkcie D, kąt prosty!
1o Znajdź równanie prostej przechodzącej przez punkty A i C, zapisz je w postaci ogólnej;
2o Znajdź długość odcinka BD czyli wysokość opuszczona z pkt−u B na podstawę AC (odległość
punktu B od prostej zawierającej wierzchołki A i C);
3o Znajdź długość odcinka AC (podstawa);
4o Podstaw do wzoru na pole Δ.
Przy punkcie D, kąt prosty!
1o Znajdź równanie prostej przechodzącej przez punkty A i C, zapisz je w postaci ogólnej;
2o Znajdź długość odcinka BD czyli wysokość opuszczona z pkt−u B na podstawę AC (odległość
punktu B od prostej zawierającej wierzchołki A i C);
3o Znajdź długość odcinka AC (podstawa);
4o Podstaw do wzoru na pole Δ.
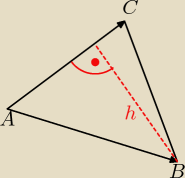 A(−4,2)
B(0,4)
C(6,−4)
Najlepiej z wektorów:
AB→=[0−(−4), 4−2]=[4, 2]
AC→=[6−(−4), −4−2]=[10, −6]
Wyznacznik wektorów:
d(AB→, AC→)=
| 4 2 |
|10 −6 |
=4*(−6)−2*10=−24−20=−44
A(−4,2)
B(0,4)
C(6,−4)
Najlepiej z wektorów:
AB→=[0−(−4), 4−2]=[4, 2]
AC→=[6−(−4), −4−2]=[10, −6]
Wyznacznik wektorów:
d(AB→, AC→)=
| 4 2 |
|10 −6 |
=4*(−6)−2*10=−24−20=−44
| 1 | 1 | |||
Pole P = | |d(AB→, AC→)|= | *|−44|=22 | ||
| 2 | 2 |
| 1 | 1 | |||
P= | ah= | *|AC|*h | ||
| 2 | 2 |
| 1 | ||
22= | *2√34*h | |
| 2 |
| 22 | |
=h | |
| √34 |
| 22√34 | 11√34 | |||
h= | = | |||
| 34 | 17 |
