? zioomalka:

	1
Wykaż że równanie (		x2−√ax+1)(x2+2x+a)=0 ma dla każdej nieujemnej wartości
	4

parametru a dokładnie dwa rozwiązania. no i stanełam na tym że wyliczyłam delty w obu nawiasach: Δ₁=a−1 dla a<0 −> Δ<0 więc brak pierwiastków równania, dla a=1 −> Δ=0 więc jeden pierwiastek równania dla a>1 −> Δ>0 wiec 2 pierwiastki równania Δ₂=4(1−a) dla a<0 −> Δ>0 są 2 rozwiązania dla a=1 −>Δ=0 jedno rozwiązanie dla a>1 −>Δ<0 brak pierwiastków równania i co teraz?

Coma13: dla a≠1 są2 pierwiastki i sama to napisałaś... a dla a=1 trzeba podstawić (1/4 * x² − x + 1)(x² + 2x + 1) = (1/2 * x −1)²(x+1)² x₁=2 x₂=−1 2≠−1 więc masz 2 pierwiastki

zioomalka: kurcze...nie rozumiem tego gdzie tu jest wykazane że nieujemne wartosci parametru a ( czyli chodzi o a>1 i a=1) mają dwa rozwiązania...mi to chyba trzeba tłumaczyć jeszcze prościej o ile sie da

Coma13: tzn patrz na Δ₁ i niżej... masz napisane dla a<0 −> Δ₁<0 więc brak pierwiastków równania a teraz patrz Δ₂ dla a<0 −> Δ₂>0 są 2 rozwiązania czyli łącznie dla a<0 masz 0 rozwiązań z pierwszego nawiasu i 2 z drugiego

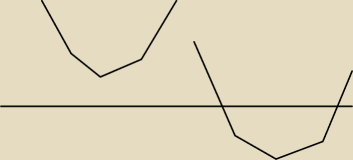
Coma13: dla a<0 to po lewej to parabola z pierwszego nawiasu

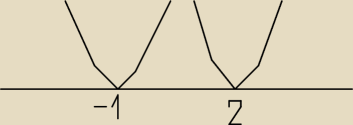
Coma13: dla a = 0

Coma13: zioomalka

zioomalka: czyli chodzi o to żeby zobaczyć ile w sumie rozwiązań mają te dwa równania w zależności od a np. a>1: przy delcie₁ sa 2 pierw. a przy delcie₂ brak czyli w sumie równanie ma 2 pierwiastki?

Coma13: tzn sama rozwiązałaś to zadanie... więc nie musisz się pytać...a zrobiłem Ci takie pseudo wykresiki więc już chyba wszystko wiesz... najważniejsze ze jak jedno równanie daje dwa x to drugie daje 0

zioomalka: no wychodzi na to że rozwiązałam coś ale sama nie rozumiałam co tak naprawdę mam w tej odpowiedzi potem napisać...haha no ale dobra już wiem (a wykresiki pierwsza klasahehe )

Coma13: a bardzo dziękuje przygotowujesz się do matury

zioomalka: tzn to nad czym sie cały czas męcze to są zadania które mają mnie powoli przygotowywać do matury ale ta czeka mnie za rok jeszcze w drugiej klasie jestem

Coma13: no ja jestem w 3 i niczego sie do tej pory nie uczyłem....myślę że nieróbstwo było błędem...

zioomalka: ale pewnie nie będzie źle a tak wracając do tych nieszczęsnych zadań: Mam obliczyć dla jakich wartości parametru m równanie x²=m(5−x) ma dwa rozwiązania o przeciwnych znakach. wiec zrobiłam tak: −x²−mx+5m=0 Δ=m²+20m żeby były dwa rozwiązania to Δ>0 wiec m²+20m>0 m₁=10 m₂=−10 i co dalej?

kaz: x₁*x₂<0

zioomalka: ale mam wyliczyć to x₁ i x₂ podstawiając pod m 10 i −10 czy jak? w odpowiedzi jest że m>0 i nie wiem jak do tego dojść...

zioomalka: a moze z wzorów Viete'a?

zioomalka: ale i tak nie wiem jak by to miało wyglądać potem...

kaz: 5m/−1<0 i część wspolna z Δ>0

zioomalka: co to jest to 5m−1<0?

kaz: 5m/−1=c/a=x₁*x₂

zioomalka: a nie moge skończyć zadania na tym ze skoro −5m ma być mniejsza od zera to m musi być>0?

kaz: z nierówności m²+20m>0→m∈(−∞,−20)v(0,+∞) 5m/−1<0→m>0 czyli m>0

zioomalka: ale i tak nie wiem w jakim celu obliczać z tej nierówności że m∈(−∞,20)v(0,∞)

zioomalka: ?

zioomalka: potrzebuje jakiegoś słownego wytłumaczenia a nie samych obliczeń...

Coma13: no tak jakby Δ>0 powoduje ze w ogóle te 2 pierwiastki istnieją.. a wzór vieta x₁*x₂<0 można sprowadzić do tego że (+)*(−)=(−) jeżeli x₁*x₂≥0 to otrzymane pierwiastki są albo dwoma liczbami ujemnymi, albo dwoma dodatnimi, albo jeden z x=0 co nie spełnia wymogów zadania... (tak możesz tłumaczyć)

kaz: aby były 2 różne pierw. Δ musi być większa od 0 i aby te pierw.miały różne znaki ich iloczyn musi być mniejszy od 0 te 2 warunki muszą być spełnione jednocześnie