funkcja;/ Alexis: Przedział (−∞; 9 〉 jest zbiorem wartości pewnej funkcji kwadratowej f. Zbiór rozwiązań nierówności f (x)≥7 jest przedziałem 〈0 ;2 〉 . Wyznacz wzór funkcji f i zapisz go w postaci ogólnej.

Artur z miasta Neptuna: y ∊ (−∞,9> wnioski z tego są następujące: 1) a < 0 2) y_w = 9 f(x) ≥7 dla x∊<0,2> wnioski z tego są następujące:

	2−0
xw =		= 1
	2

wzór ogólny: y= a(x−p)² + q .... gdzie p = −x_w .... oraz q = y_w

Artur z miasta Neptuna: tfuuu p = x_w

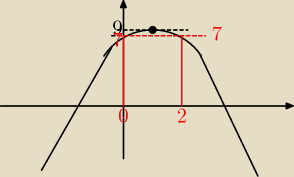
think: wiesz, że ramiona ma skerowane w dół, wierzchołek w 9 f(0) = 7 f(2) = 7 a to nam daje wsółrzędne wierzchołka (1, 9) wynika to z symetrii paraboli, wzór na postać kanoniczną f(x) = a(x − 1)² + 9 to podstaw f(0) = 7 7 = a(0 − 1)² + 9 → a = ...?

Alexis: a=−2

Alexis: skad think masz wierzcholek 1,9 ?

think: skoro zbiór wartości funkcji to (−∞, 9> to tak się składa że zbiór wartości jest w zależności od tego w którą stronę są skierowane ramiona zapisywany jako (−∞, q> lub przy ramionach w górę <q, ∞) także druga współrzędna wierzchołka paraboli jest znana od razu. Natomiast pierwsza

	0 + 2
współrzędna to średnia z		= ...
	2

zauważ, że jak byś znał/−a miejsca zerowe paraboli to wierzchołek leży dokładnie po środku, PARABOLA JEST SYMETRYCZNA względem wierzchołka

Olga: ok