:( Bobek: Mógłby ktoś rozwiązać Półkolisty arkusz blachy o średnicy 64 cm, zawinięto w lej o kształcie stożka. Oblicz pojemność tego naczynia (zakładając,że jest ono szczelne). Ile będzie ważył olej o gęstości 2,4 g/cm³, którym całkowicie napełniono to naczynie.

tim: Masz odpowiedzi?

Coma13: tzn pytanie jest czy powstaną jakieś zakładki... i czy całe pole powierzchni półkola stanie się polem powierzchni ściany bocznej....?

tim: Wychodzą mi kosmiczne liczby z π.

Bogdan: Podpowiedź. Jeśli półkole o promieniu R jest powierzchnią boczną stożka, to przekrojem osiowym stożka jest trójkąt równoboczny o boku R.

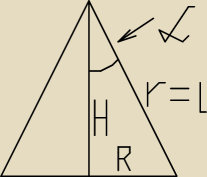
Coma13: mi się wydaje że P_k/2 = P_{ściany bocznej} = πr²/2 = 512π 1/2 Obwodu koła = πr = 32π = 2πR gdzie R−pole powstałego stożka R=16 małe r jest teraz tworząca stożka czyli r=l=32 sinα=R/r=1/2 czyli przekrój stożka jest trójkątem równobocznym więc H=a√3/2 = 16√3 V=1/3 * πR² * H = 1/3 * 256π * 16√3 = 4096π√3/3 (możesz to sobie przybliżyć m=gęstość * V = 2,4 * V = 3276,8 g

Coma13: m = 3276,8π grama jeżeli już

tim: Więc tak: l = 32 = r Obwód półkola = πr = 32π Obwód półkola = Obwód podstawy stożka 32π = 2πR = R = 16 Pole podstawy stożka. πr² = 256π H = 16√3 [patrz Coma13] Można też tak.

Coma13: m = 3276,8π√3 − chyba już o niczym nie zapomniałem... na papierze się łatwiej pisze

Coma13: w każdym razie H i R się zgadzają... więc jest okey