średnia geometryczna
wjmm: Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średnie
geometrycznej długości podstaw trapezu.
Taka średnica to musi być wysokością tego trapezu. Czyli jeśli przyjmiemy sobie, że
wysokość to h, a postawy a i b, to po wykonaniu odpowiednich równań musi wyjść:
h=
√a*b. A mi wychodzi cały czas h=
√a*b/2. Czy coś źle robię

10 kwi 13:54
Bogdan:
Zaraz pokażę
10 kwi 14:07
s:
dssdπsd
10 kwi 14:14
Bogdan:
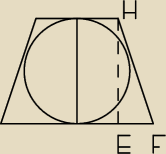
a, b − podstawy trapezu, a > b,
h = 2r − wysokość trapezu i średnica okręgu wpisanego w ten trapez,
c =
12(a + b) − ramię trapezu
Jeśli czworokąt jest opisany na okręgu, to sumy długości przeciwległych boków
są sobie równe, czyli a + b = 2c
W widocznym trójkącie prostokątnym EFH:
|EF| =
a−b2
|HE| = h,
|HF| =
a+b2
Korzystając z wzoru Pitagorasa wyznacz w tym trójkącie h.
10 kwi 14:19
Bogdan:
Pytanie do wszystkich.
Które odcinki w omawianym trapezie o podstawach a, b (a > b) mają długość równą
średniej arytmetycznej długości podstaw oraz średniej harmonicznej długości podstaw.
10 kwi 14:23
tim:
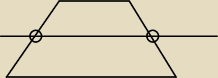
Od połówek bocznych krawędzi?
10 kwi 14:25
Bogdan:
Tak tim, to jest odcinek o długości średniej arytmetycznej podstaw, ale w omawianym
trapezie nie jedyny o tej własności, gdzie jest inny?
I gdzie jest odcinek o długości średniej harmonicznej podstaw a, b.
10 kwi 14:33
tim: Jakbym wiedział, co to średnia harmoniczna..?
10 kwi 14:37
tim: Do I. Jeszcze krawędzie?
10 kwi 14:38
Bogdan:
s
H − średnia harmoniczna n liczb liczb: a
1, a
2, ... , a
n
| | n | |
sH = |
|
|
| | 1a1 + 1a2 + ... + 1an | |
Dla dwóch liczb a, b;
s
H =
2aba + b
10 kwi 15:04
tim: To nie wiem
10 kwi 15:06
Bogdan:
Tak tim, w omawianym trapezie również ramiona mają długość równą średniej
arytmetycznej podstaw.
10 kwi 15:06
Bogdan:
tim, rozwiąż następujące zadanie.
Z miejscowości A do miejscowości B samochód jedzie z średnią prędkością
v1 = 20 km/h, a drogę powrotną tą samą trasę, czyli z B do A samochód pokonuje
z średnią prędkością v2 = 80 km/h.
Oblicz średnią prędkość na trasie A−B−A.
10 kwi 15:09
tim: Proste

, należy pamiętać, że w takich zadaniach, nigdy nie będzie to śr. arytmetyczna
20 i 80

| | 2S | | 2S | | 2s | |
Vśr = |
| = |
| = |
| = |
| | t1 + t2 | | | | | |
Czyż nie?
10 kwi 15:21
Bogdan:
Dobrze tim.
vs = 2*20*8020 + 80 = 32
A mówiłeś, że nie znasz średniej harmonicznej
10 kwi 15:26
tim: Bo nie znam

, tzn nie wiedziałem, że to to... Bo takie zadania to konkursowe zawsze,
więc trzeba umieć

10 kwi 15:31
Bogdan:
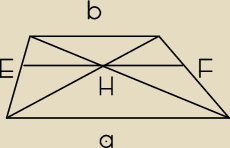
W dowolnym trapezie odcinek równoległy do podstaw i przechodzący przez punkt
przecięcia przekątnych ma długość równą średniej harmonicznej długości podstaw.
|EF| =
2aba + b
|EH| = |HF| =
aba + b
10 kwi 15:46
tim: Ciekawe

, nie słyszałem nigdy

10 kwi 15:53
wjmm: To ja wiem jak wyznaczyć h (dokładnie jak napisałeś), ale to h nie jest średnią
geometryczną

11 kwi 16:02
Bogdan:
Rozpatrujemy trójkąt prostokątny HEF (rysunek wyżej)
h = 2r,
h − wysokość trapezu,
r − długość promienia okręgu wpisanego w trapez rownoramienny
a, b − podstawy trapezu, a > b.
Z twierdzenia Pitagorasa: |HE|2 = |HF|2 − |EF|2
h2 = (a+b2)2 − (a−b2)2
h2 = (a+b2 + a−b2) * (a+b2 − a−b2)
h2 = ab.
Jeśli mamy ciąg (cn): c1 = a, c2 = h, c3 = b lub c1 = b, c2 = h, c3 = a
oraz spełniona jest równość: h2 = ab, to ciąg (cn) jest ciągiem geometrycznym,
natomiast h jest średnią geometryczną a oraz b.
wjmm wyjaśnij, co miałeś na myśli, mówiąc, że h nie jest średnią geometryczną.
11 kwi 19:06

 dssdπsd
dssdπsd
 a, b − podstawy trapezu, a > b,
h = 2r − wysokość trapezu i średnica okręgu wpisanego w ten trapez,
c = 12(a + b) − ramię trapezu
Jeśli czworokąt jest opisany na okręgu, to sumy długości przeciwległych boków
są sobie równe, czyli a + b = 2c
W widocznym trójkącie prostokątnym EFH:
|EF| = a−b2
|HE| = h,
|HF| = a+b2
Korzystając z wzoru Pitagorasa wyznacz w tym trójkącie h.
a, b − podstawy trapezu, a > b,
h = 2r − wysokość trapezu i średnica okręgu wpisanego w ten trapez,
c = 12(a + b) − ramię trapezu
Jeśli czworokąt jest opisany na okręgu, to sumy długości przeciwległych boków
są sobie równe, czyli a + b = 2c
W widocznym trójkącie prostokątnym EFH:
|EF| = a−b2
|HE| = h,
|HF| = a+b2
Korzystając z wzoru Pitagorasa wyznacz w tym trójkącie h.
 Od połówek bocznych krawędzi?
Od połówek bocznych krawędzi?
 , należy pamiętać, że w takich zadaniach, nigdy nie będzie to śr. arytmetyczna
20 i 80
, należy pamiętać, że w takich zadaniach, nigdy nie będzie to śr. arytmetyczna
20 i 80
 , tzn nie wiedziałem, że to to... Bo takie zadania to konkursowe zawsze,
więc trzeba umieć
, tzn nie wiedziałem, że to to... Bo takie zadania to konkursowe zawsze,
więc trzeba umieć 
 W dowolnym trapezie odcinek równoległy do podstaw i przechodzący przez punkt
przecięcia przekątnych ma długość równą średniej harmonicznej długości podstaw.
|EF| = 2aba + b
|EH| = |HF| = aba + b
W dowolnym trapezie odcinek równoległy do podstaw i przechodzący przez punkt
przecięcia przekątnych ma długość równą średniej harmonicznej długości podstaw.
|EF| = 2aba + b
|EH| = |HF| = aba + b
 , nie słyszałem nigdy
, nie słyszałem nigdy 
