wielomiany, stereometria, analityczna, dowód Olówka: mam problem z kilkoma zadaniami. 1. Punkty A=(−5,5), C=(8,6) są przeciwległymi wierzchołkami trapezu równoramiennego ABCD, w którym AB jest równoległe do CD. Prosta o równaniu y=2x jest osią symetrii tego trapezu. Oblicz współrzędne wierzchołków B i D oraz pole tego trapezu. 2. W ostrosłupie trójkątnym ABCS o podstawie ABC i wierzchołku S dane są AB=AC=SB=SC=9 i AS=BC=8. Oblicz objętość ostroslupa. 3. Wykaż, że nie istnieje wielomian stopnia trzeciego o współczynnikach całkowitych, który spełnia warunki: W(2)=3, W(−2)=2. Nie wiem jak mam zapisać "szkielet" wielomianu stopnia trzeciego. 4. Dany jest trójkąt ostrokątny ABC o bokach a, b, c i kątach α,β,γ. Wykaż, że b²+c²−a²/a⁺c²−b²=tgbeta/tgalfa. Będę bardzo wdzięczna za pomoc w tych zadankach. Przepraszam za słowne nazwy kątów ale cos popsułam i nie chce wyjść inaczej pozdrawiam i życzę miłego wieczoru

ejendi: 1.)A=(−5,5), C=(8,6) B(7,−1) D(0,10) P=75 AB⊥ do y=2x przez A y−5=−0,5(x+5); y=−0,5x+2,5 ⊥ do y=2x przez C y=−0,5x−3+8=−0,5x+5 E przecięcie y=2x z AB E(1,2) F przecięcie y=2x z CD F(4,8) B(2*Ex−Ax,2*Ey−Ay)=(2+5,2*2−5)=(7,−1) podobnie D(0,10) h=|EF| a=|AB| b=|CD| itd...

Mila: 3) w(x)=ax³+bx²+cx+d z warunków zadania 8a+4b+2c+d=3 −8a+4b−2c+d=2 dodajemy stronami 8b+2d=5

	5
d=		−4b
	2

zrób analizę wyrażenia i daj odpowiedź.

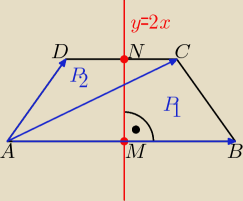
Gustlik: 1. Punkty A=(−5,5), C=(8,6) są przeciwległymi wierzchołkami trapezu równoramiennego ABCD, w którym AB jest równoległe do CD. Prosta o równaniu y=2x jest osią symetrii tego trapezu. Oblicz współrzędne wierzchołków B i D oraz pole tego trapezu. Wyznaczam równanie prostej AB zawierajacej podstawę "dolną" tego trapezu:

	1
a=−		− z warunku prostopadłości do prostej y=2x
	2

Wstawiam współrzędne p−tu A leżącego na tej prostej: y=−U{1]{2}x+b₁

	1
5=−		*(−5)+b1
	2

	5
5=		+b1
	2

	5
b1=
	2

	1		5
pr. AB: y=−		x+
	2		2

Wyznaczam współrzędne środka M podstawy AB: {y=2x

	1		5
{y=−		x+
	2		2

	1		5
2x=−		x+		/*2
	2		2

4x=−x+5 5x=5 /:5 x=1 y=2 M=(1, 2) A=(−5,5)

	−5+xB		5+yB
M=(		,		)
	2		2

−5+xB
	=1 /*2
2

−5+x_B=2 x_B=7

5+yB
	=2 /*2
2

5+y_B=4 y_B=−1 B=(7, 1) Wyznaczam równanie prostej CD zawierającej "górną" podstawę tego trapezu: y=−U{1]{2}x+b₂ − z równoległości do AB ten sam wsp. kierunkowy Wstawiam wsp. C=(8,6) leżącego na niej:

	1
6=−		*8+b2
	2

6=−4+b₂ b₂=10 Pr. CD: y=−U{1]{2}x+10 Liczę wsp. p−tu N będącego środkiem CD {y=2x {y=−U{1]{2}x+10 2x=−U{1]{2}x+10 /*2 4x=−x+20 5x=20 /:5 x=4 y=8 N=(4, 8) C=(8,6)

	8+xD		6+yD
N=(		,		)
	2		2

8+xD
	=4 /*2
2

8+x_D=8 x_D=0

6+yD
	=8 /*2
2

6+y_D=16 y_D=10 D=(0, 10) Trapez ma wierzchołki: A=(−5,5) B=(7, 1) C=(8,6) D=(0, 10) Dzielę trapez wektorami na trójkąty ABC i ACD i liczę ich pola z wyznacznika wektorów: AB^→=[7−(−5), 1−5]=[12, −4] AC^→=[8−(−5), 6−5]=[13, 1] AD^→=[0−(−5), 10−5]=[5, 5] Liczę wyznacznik d₁=d(AB^→, AC^→) d₁= | 12 −4 | | 13 1 | =12*1−(−4)*13=12+52=64

	1
Pole ΔABC=P1=		|d1|=32
	2

Liczę wyznacznik d₂=d(AC^→, AD^→) d₁= | 13 1 | | 5 5 | =13*5−1*5=65−5=60

	1
Pole ΔACD=P2=		|d2|=30
	2

Pole trapezu = P₁+P₂=32+30=62 Na wszelki wypadek proszę o sprawdzenie, czy nie popełniłem błędów rachunkowych, bo obliczeń było sporo. Ale na pewno taką metodą mozna to rozwiazać.

Gustlik: Sorki, zauważyłem błąd: Trapez ma wierzchołki: A=(−5,5) B=(7, −1) C=(8,6) D=(0, 10) Dzielę trapez wektorami na trójkąty ABC i ACD i liczę ich pola z wyznacznika wektorów: AB→=[7−(−5), −1−5]=[12, −6] AC→=[8−(−5), 6−5]=[13, 1] AD→=[0−(−5), 10−5]=[5, 5] Liczę wyznacznik d1=d(AB→, AC→) d1= | 12 −6 | | 13 1 | =12*1−(−6)*13=12+78=90

	1
Pole ΔABC=P1=		*|d1|=45
	2

Liczę wyznacznik d2=d(AC→, AD→) d1= | 13 1 | | 5 5 | =13*5−1*5=65−5=60 Pole ΔACD=P2=U{1]{2}|d2|=30 Pole trapezu = P1+P2=45+30=75 Teraz powinno być dobrze, ale proszę jeszcze sprawdzić.

Mila: 4) jutro, dobranoc