Najdłuższa przekątna graniastosłupa prawidłowego sześciokątnego ma długość p Rafik: Rozwiązuje zadania do jutrzejszego sprawdzianu ze stereometrii i cienko mi to idzie... Między innymi tego zadania nie mogę rozgryźć, będę wdzięczny za pomoc. Kombinowałem coś z wysokością trójkąta równobocznego i funkcjami tryg. (cosinusem) ale nie idzie... Najdłuższa przekątna graniastosłupa prawidłowego sześciokątnego ma długość p i tworzy z krótszą przekątną podstawy wychodzącą z tego samego wierzchołka kąt o mierze α. Oblicz objętość graniastosłupa. Dla jakich α zadanie ma rozwiązanie.

Rafik: Błagam pomóżcie,jutro mam sprawdzian! : (((

Mila: α∊(π/3,π/2) masz odpowiedź na objętość, czy Ci napisać?

Mila: Podaj mi odpowiedź, bo nie wiem, czy nie mam błędu rachunkowego.

Rafik: V=^p3_/2cos²α√4sin²α−1, α(^pi₆,^pi₂) Prosiłbym o całe rozwiązanie krok po kroku, muszę wiedzieć skąd co się wzięło

Mila: Zrobisz rysunek z oznaczeniami? czy ja mam zrobić?

Mila:

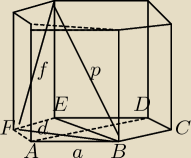
Mila: d=a√3 krótsza przekątna podstawy , KątFBE'=α , wierzchołki u góry A',B', C' D'E'F' H²+(2a)²=p² w ΔE'EB H − wysokość gran. ⇔H²=p² −4a² f²=a²+H² w ΔFEE' wΔFBE': f²=p²+d²−2pdcosα ⇔a²+H² =p²+d²−2pdcosα a²+p² −4a²=p²+d²−2pdcosα podstaw za d i oblicz a spróbuj dalej policzyć, wszystko ładnie wyjdzie. α∊(π/6,π/2) Jak będą kłopoty to napiszę, ale to się źle pisze.

Millenium: ok dzięki wielkie,musiał mnie ktoś naprowadzić Dalej powinienem sobie poradzić. DZIĘKUJĘ : ))

Mila:

trel: Mógłby mi ktos to rozpisać, będzę wdzięczzna.

trel: Mi wszło tak: V= 1/2 * ^{p √ 3} _{3+3p²−2√ 3} cosα * (p² − ^4p _{3+3p²−2√3}cosα)

trel: 1/2 * nad kreską: p √3, pod kreską: 3+3p² − 2√3cosα * p² − nad: 4p, pod kreską:3+3p² − 2√3cosα. Napisałam tak, bo nic nie widać wcześniej

trel: V= 1/2 * ^{p √ 3} _{3+3p²−2√ 3} cosα * (p² − ^4p _{3+3p²−2√3}cosα)

trel: Pomoże ktoś?

Mila: Czego nie rozumiesz, to było tak dawno, że muszę od początku rozwiązywać.

trel: Nie wiem czy dobrze mi wyszło?

trel: a, wiem, mam źle, bo niepotrzebnie podzieliam to wszystko przez 3!

trel: ale nie wiem czy mimo tego nie zrobiłam jezcze jakiegoś błędu.

Mila: Jakie masz a? Jaka masz H?

trel: a² = p²/(3+3p²−2√3cosα)

Mila: Zaczynam od wzoru: a²+p² −4a²=p²+d²−2pdcosα ⇔ −3a²=d²−2pd cosα i d=a√3 −3a²=3a²−2p*a√3*cosα⇔ 6a²=2p*a*√3*cosα

	√3*p*cosα
a=
	3

================

	p2*cos2α
H2=p2−4a2=p2−4*
	3

	4cos2		3−4cos2α
H2=p2(1−		)=p2*(		)
	3		3

	√3−4cos2α
H=p*
	√3

======================

	a2√3
VGran.= 6*		*H
	4

	p2*cos2α*√3		√3−4cos2α
=6*		*p*
	3*4		√3

	p3*cos2α*√3−4cos2α
VGran.=
	2

	π		π
α∊(		,		)
	6		2

trel: ok, dzieki wielkie mam jeszcze jedno pytanie dotyczące kata. Zrobiłam, że to co pod pierwiastkiem musi być wieksze od zera. Dlaczego odrzucam − √3/2 ?

Mila: Ujemne wartości cosinus przyjmuje dla kątów rozwartych.

trel: a dlaczego do 45 st a nie 90?

Mila: Badasz wyrażenie pod pierwiastkiem.

π
	=90o. Nie ma tam kąta 45o.
2