trapez Magda: Pytanie: Czy w trapezie równoramiennym punkt przecięcia się przekątnych to środek koła opisanego na nim?

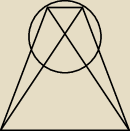
sla1: chyba nie za bardzo...

Magda: To podam takie zadanie co chyba opiera się na tym, ale może z czegoś innego to się bierze. Podstawą ostrosłupa jest trapez równoramienny o podstawach a, 3a i kącie ostrym α. Krawędzie boczne są nachylone do podstawy pod tym samym kątem α. Oblicz objętość ostrosłupa.

Magda: zrobi ktoś to zadanie?

pigor: środek okręgu opisanego na trapezie np. ABCD , to zarazem środek okręgu opisanego na ΔABC lub ACD i ... tyle. ...

rumpek: Skoro krawędzie są nachylone do płaszczyzny podstawy, czyli punktem wysokości jest środka okręgu opisanego na podstawie (w tym wypadku trapezie równoramiennym). 1^o Obliczmy wpierw pole podstawy:

	(a + b)h
P =
	2

	4ah
P =
	2

Pozostało wyliczyć, h nie jest to trudne (musisz odpowiednie oznaczenia wprowadzić na obrazek) Oznaczmy sobie krótsza podstawę jako g, oznaczmy sobie dłuższa podstawę jako f. Wiemy ponadto, że g = a oraz f = 3a. Dłuższa podstawę możemy określić jako: f = g + 2x, czyli: 3a = a + 2x ⇒ 2a = 2x ⇒ x = a. Pozostało skorzystać z funkcji trygonometrycznych:

	h
tgα =		⇒ h = tgαx ⇒ h = tgαa
	x

	4a * tgαa
P =
	2

P = 2a²tgα Zaraz dokończę

rumpek: Albo napiszę jak dokończyć Liczysz z tw. Pitagorasa przekątną |BD| (w trójkącie BDE) p² = h² + (2a)² p² = tg²αa² + 4a² p² = a²(tg²α + 4), p∊R₊ p = a√tg²α + 4 Potem możesz wykorzystać tw. sinusów

	p
2R =
	sinα

	a√tg2α + 4
2R =		/ : 2
	sinα

	a√tg2α + 4
R =
	2sinα

Dalej tylko z zależności trygonometrycznych

	H
tgα =
	R

...

rumpek: Lub można policzyć przekątną |BD| z tw. cosinusów Lecz do tego będziemy potrzebowali |AD|.

	|AD|
cosα =
	x

|AD| = acosα p² = (acosα)² + (3a)² − 6a²cos²α p² = a²cos²α + 9a² − 6a²cos²α p² = 9a² − 5a²cos²α p² = a²(9 − 5cos²α), p∊R₊ p = a√9 − 5cos²α I potem podobnie

Magda:

	H
Wszystko ok, ale nie widze tego że tgα=		, mógłbyś rumpek to narysować ?
	R

rumpek: Nie mam talentu do rysunków, gdzie trapez jest w podstawie także lepiej nie będę próbował