dział: twierdzenie Talesa
******POLA******POLA PAOLA***********************: 10.21* trójkąt ostrokątny ABC, w którym |<BCA|=α, |<ABC|=β (β<α) ma pole P. Oblicz pole
wyciętego z trójkąta ABC przez wysokość i dwusieczną kąta poprowadzone z wierzchołka C.
wszystkim życzę wesołych świąt

10 kwi 10:46
b.:
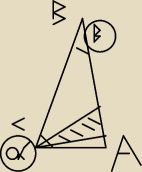
Zrobiłem sobie rysunek (w kółkach miary kątów: α i β), ale nie widzę, jak to rozwiązać...
10 kwi 18:51
tim: b. Witamy w święta.
Miałem to samo uczucie

10 kwi 18:51
b.: Trochę dziwne, że przy wierzchołku C kąt ma miarę α −− treść ok?
10 kwi 18:52
b.: Znowu zaproponuję niezbyt ładne rozwiązanie

niestety, jestem słaby w geometrii...
Oznaczmy dodatkowo przez D spodek wysokości opuszczonej z C, a przez E − punkt wspólny
dwusiecznej kąta przy C i boku AB.
| | |DE| | |
Szukane pole trójkąta CDE = P * |
| |
| | |AB| | |
wystarczy więc wyrazić ten iloraz poprzez (funkcje trygonometryczne) α i β −− a to da się
zrobić korzystając kilkukrotnie z tw. sinusów
a najpierw należy powyliczać miary kątów np. w trójkącie CDE
−−−−−−−
Jeśli to Ci Polu nie wystarczy, spróbuj wyliczyć miary kątów w trójkącie CDE i napisz,
ile Ci wyszło.
10 kwi 19:19

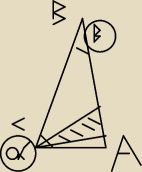 Zrobiłem sobie rysunek (w kółkach miary kątów: α i β), ale nie widzę, jak to rozwiązać...
Zrobiłem sobie rysunek (w kółkach miary kątów: α i β), ale nie widzę, jak to rozwiązać...

 niestety, jestem słaby w geometrii...
Oznaczmy dodatkowo przez D spodek wysokości opuszczonej z C, a przez E − punkt wspólny
dwusiecznej kąta przy C i boku AB.
niestety, jestem słaby w geometrii...
Oznaczmy dodatkowo przez D spodek wysokości opuszczonej z C, a przez E − punkt wspólny
dwusiecznej kąta przy C i boku AB.