??
Jak to spr?: funkcja f(x)= −(x−2)2+b nie ma miejsc zerowych dla:
a) b=0
b) b=4
c) b<0
d) b>0
18 mar 15:14
Aga1: c
18 mar 15:18
pomagacz:
najlepiej sprowadzić do postaci ogólnej funkcji
f(x) = −x2 + 4x + (−2 + b)
Δ = b2 − 4ac < 0
16 + 4(−2 + b) < 0
...
18 mar 15:19
Tragos: ramiona paraboli skierowane do dołu
aby nie miała miejsc zerowych cała parabola musi być pod osią OX
czyli funkcję y= −x2 trzeba przesunąć w dół
b < 0
−−−−−−−−−
można też inaczej
f(x) = −(x2 − 4x + 4) + b = −x2 + 4x + b − 4
Δ = 16 − 4*(−1)*(b−4) = 16 + 4(b − 4) = 16 + 4b − 16 = 4b
Δ < 0
4b < 0
b < 0
18 mar 15:20
Aga1: Albo
−(x−2)2=−b//:−1
(x−2)2=b−−−równanie nie ma rozwiązania, gdy b<0
18 mar 15:32
MATMA: gdyby to rozwiązać to delta wyszłaby równa 0
(x−2)2=b
18 mar 15:37
pomagacz:
oj ludziska, przecież równanie kwadratowe nie ma (w liceum) rozwiązań, gdy Δ < 0

18 mar 15:44
MATMA: ale ma gdy Δ=0
18 mar 15:46
Tragos: (x−2)2 = b
(coś do kwadratu)2 = coś ujemne
brak rozwiązań, więc b musi być ujemne, czyli b < 0....................
18 mar 15:47
Aga1: Możesz liczyć , ale po co?
x2−4x+4−b=0
Δ=16−4(4−b)=16−16+4b=4b
Δ<0⇔4b<0⇔b<0
Czy liczysz Δ gdy masz równanie np. x2=−4?
18 mar 15:51
Eta:
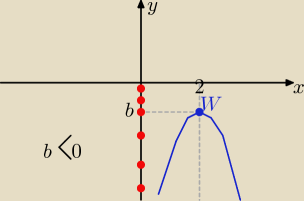
18 mar 15:51
Tragos: oczywiście rozwiązując w liczbach rzeczywistych
18 mar 15:51
pomagacz:
brak miejsc zerowych
f(x) = −(x − 2)2 + b
f(x) = −(x − p)2 + q
ramiona w dół
W = (p, q) ⇒ q < 0
czyli:
b < 0
18 mar 15:52

