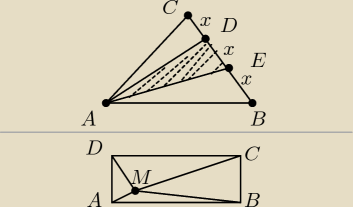
Zadania na dowodzenie mark: Mam 2 zadania z geometrii. Nie bardzo mam pomysł jak się za każde zabrać. Obydwa na dowodzenie

	1
1. T: PΔADE =		PΔABC
	3

boki różnej długości 2. T: |AM|² + |CM|² = |BM|² + |DM|² Z góry dziękuje za pomoc

MQ: ad. 1 Pole trójkąta to 1/2*podstawa*wysokość. Przyjmij za podstawy CB i DE, a wszystko będzie jasne.

MQ: Ad. 2 Czy M jest dowolnym punktem?

mark: ad.1 dzięki wyszło ad.2 tak, dowolnym

pigor: ... np. poprowadź przez M odcinki równoległe do AB i BC odpowiednio i przyjmując długości odpowiednich odcinków (dla uproszczenia zapisu) ... "pobaw się" 4 razy twierdzeniem . Pitagorasa . ...

MQ: Już wiem: Wystarczy poprowadzić przez M odcinek równoległy do AD (równoległy też do CD). U góry dostaniemy punkt M₁ U dołu punkt M₂ DM²=DM₁²+M₁M² i tak dalej Wszystko wychodzi jak sobie dodasz AM² i CM² i tak samo BM² i DM²

mark: Dzięki