Trójkąt obracamy wokół osi równoległej do boku AB Millenium: W trójkącie ABC bok AB ma długość a, natomiast kąty ostre do niego przyległe mają miary alpha i beta. Trójkąt ten obracamy wokół osi równoległej do boku AB i przechodzącej przez wierzchołek C. Oblicz objętość otrzymanej bryły obrotowej. HELP!

Millenium:

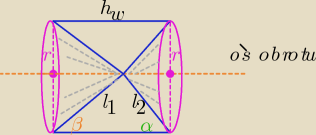
Eta: Jaki to trójkąt? prostokątny? ( bo nie napisałeś) Powstałą bryłą jest walec z wydrążonymi w podstawach walca stożkami o różnej objętości gdzie: r(st₁)= r(st₂) V(br) = W(walca) − V(st₁) − V(st₂)=......

Millenium: nie ma powiedziane w zadaniu jaki to trójkąt więc chyba różnoboczny.

Millenium: A mogę prosić o wszystkie obliczenia, bo nie bardzo wiem jak to zrobić. Wydaje mi się, że trzebaby tu było wprowadzić jakiś parametr ale nie wiem za co? Myślałem nad hw − (odleglosc od spadku wysokości do wierzchołka większego kąta) ale nie bardzo mi tak wychodzi.

Rafik: PROSZĘ : )))))))

Millenium: Czy mógłby ktoś podać całe rozwiązanie?

Mila: α+β<180 z Tw. sinusów:

l1		a
	=
sinα		sin(α+β)

l2		a
	=
sinβ		sin(α+β)

	ha
sinα=
	l2

oblicz h_a z tych zależności i masz promien .

Millenium: czemu tam jest sin(α+β)

Mila: γ=180−(α+β) sin(180−(α+β))=sin(α+β)