wektor maja: Poproszę o sprawdzenie M(127,−342).Wektor MN=[4,7].Oblicz współrzędne punktu N. rozw:N(x,y) MN=[127−x,−342−y] MN=[4,7] (127−x=4) i (−342−y=7) 127−4=x x=123 −342−7y y=−349

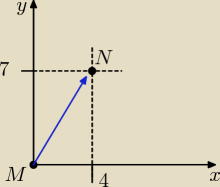
ejendi: N(127+4,−342+7)=(131,−335)

maja: bardzo dziękuję ,,ejendi",wszystkiego naj...ci zyczę

maja: a czy pomozesz mi jeszcze?bo nie dam rady:Q(2,1)jest punktem przecięcia przekątnych r ównoległoboku ABCD. wektor Qa=3a=b, zaśQB=2a−3b, gdzie a=[1,0], b=[0,1].Znajdz wierzchołki tego równoległoboku.

pigor: ... np. tak : Q=(2,1) QA=3[1,0]+[0,1]=[3,0]+[0,1]= [3,1] i QB=2[1,0]−3[0,1]=[2,0]+[0,−3]= [2,−3] , więc A=(x,y) ⇒ QA=[x−2,y−1]=[3,1] ⇔ x−2=3 i y−1=1 ⇔ x=5 i y=2 ⇒ A=(5,2) , B=(x,y) ⇒ QB=[x−2,y−1]=[2,−3] ⇔ x−2=2 i y−1=−3 ⇔ x=4 i y=−2 ⇒ B=(4,−2) , zatem ze wzoru na środek odcinka C=(x,y) ⇒ x+5=2*2 i y+2=2*1 ⇔ x=−1 i y=0 ⇒ C=(−1,0) , D=(x,y) ⇒ x+4=2*2 i y−2=2*1 ⇔ x=0 i y=4 ⇒ D=(0,4) ... i to tyle . ...

ejendi: lepiej późno niż wcale, powodzenia a=[1,0], b=[0,1]. QA=3a+b (chyba tak bo= jest pod +) QA=(3,1) ten wektor dodajemy do Q i mamy A Q+QA=A=(Qx+3ax+bx,Qy+3ay+by)=(2+3*1+0,1+3*0+1)=(5,2) QB=2a−3b QB=(2*ax−3bx,2ay−3by)=(2,−3) Q+QB=B=(2+2,1−3)=(4,−2) Aby otrzymać C i D dodajemy wektory przeciwne −QA=(−3,−1) i −QB=(−2,3) C=Q−QA=(2−3,1−1)=(−1,0) D=Q−QB=(2−2,1+3)=(0,4)