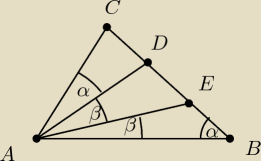
Udowodnić tezę w trójkącie mark: Muszę udowodnić tezę: |AC| = |CE| i nie mam pojęcia jak się za to zabrać. Będę bardzo wdzięczny za jakieś wskazówki

rumpek: * zakładam, że |AE| jest dwusieczną skoro masz udowodnić, że trójkąt ACE jest równoramienny (|AC| = |CE|) to wystarczy na podstawie kątów Tak jak masz na rysunku oznaczenia . To teraz rozpatrzmy kąt |∡AEB| w trójkącie ABE, ten kąt to po prostu: |∡AEB| = 180 − α − β = 180^o − (α + β). To teraz rozpatrzmy kąt |∡AEC| w trójkącie ACE jest ten kąt równy |∡AEC| = α + β, ponieważ https://matematykaszkolna.pl/strona/2886.html To widzimy, że ma dwa katy takie same, więc boki podane w tezie są równe c.n.u.

Mila: Kąt AEC jest kątem zewnętrznym dla ΔAEB i w takim razie jest równy sumie kątów nieprzyległych do niego , czyli α+β. I to już koniec.

mark: Dzięki! Teraz wydaje się to oczywiste

Ted: zobacz czemu równa się ∡AEC ...−