Goema Zadanko: 1. W trójkącie prostokątnym spodek wysokości, poprowadzonej z wierzchołka kąta prostego podzielił przeciwprostokątną na odcinki długości:√6 i 9√6 . Oblicz a. długość wysokości poprowadzonej z wierzchołka kąta prostego b. długości przyprostokątnych c. odległość środka ciężkości trójkąta od wierzchołka kąta prostego. d. pole trójkąta e. promień okręgu wpisanego w trójkąt f. promień okręgu opisanego na trójkącie 2. Oblicz długość promienia okręgu wpisanego w trójkąt równoboczny, jeśli a. wysokość trójkąta ma długość 21 cm b. bok trójkąta ma długość 10 cm c. środek ciężkości tego trójkąta leży w odległości 5 cm od wierzchołków tego trójkąta 3. W trójkącie równoramiennym ABC podstawa AB ma długość 10 cm. Odcinek AD jest wysokością tego trójkąta. Widząc, że |DB| = 6 cm oblicz obwód trójkąta ABC 4. W prostokącie ABCD poprowadzono odcinek AE prostopadły do przekątnej DB i punkt E należy do boku DC prostokąta Przekątna DB przecina się z odcinkiem AE w punkcie P. Wiedząc, że |AP| = 8 cm, |PE| = 2 cm, oblicz: a. długość przekątnej prostokąta b. długość boków prostokąta

Aga1: a)h²=√6*9√6 h=

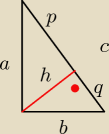
Aga1: a) p=9√6, q=√6 h²=p*q b)b²=h²+q² a²=h²+p²

	1
d) P=		ab
	2

	1
f)R=		c, c=p+q.
	2

	a+b−c
e)r=
	2