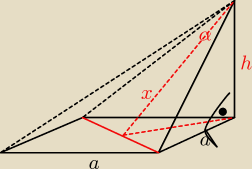
stereometria koń rafał: Hej, czy ktoś mógłby mi pomóc z tymi zadaniami: 1. Podstawą ostrosłupa jest kwadrat o boku długości a. Jedna z jego krawędzi bocznych jest prostopadła do plaszczyzny podstawy. Przekątną podstawy, która łączy końce równych krawędzi bocznych, widać z wierzchołka ostroslupa pod kątem α. Wyznacz objętość ostrosłupa. 2. Podstawą ostrosłupa jest trójkąt równoboczny o boku dlugości a. Dwie ściany tego ostrosłupa są prostopadłe do podstawy, zaś trzecia tworzy z płaszczyzną kąt α. Wyznacz pole powierzchni bocznej ostrosłupa. 3. W ostrosłupie prawidłowym czworokątnym pole jednej ściany bocznej jest równe S, zaś kąt płaski przy wierzchołku ściany bocznej równy jest 2α. Wyznacz V.

sla1: V=¹₃*a²*h

sla1:

	α		a√2   2
Mamy dany kat α i krawędzie boczne: tg		=		stąd
	2		x

	a√2
x=
	2tgα2

	a√2
x2=(		)2+h2
	2

2a2		2a2
	=		+h2,
α   4tg2   2		4

stąd po obliczeniach

	a(1−tg2α2)(1−tg2α2)
h=
	√2tgα2

podstawiamy pod wzór na V=¹₃*a²*h

koń rafał: dziękuję

sla1:

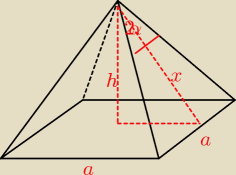
	1		x		1		a		x
h=H. zad3.V=		a2H, ctgα=		, S=		ax=		x, ctgα=		,
	3		a   2		2		2		a   2

	a		a		a		2S		a
x=		ctgα, S=		*		ctgα, 4S=a2ctgα, stąd a=		,TERAZ x=		ctgα,
	2		2		2		ctgα		2

	a		a		a2		a2		a2
H2=x2−(		)2,więc H2=(		)2ctg2α−		, H2=		ctg2α−		,
	2		2		4		4		4

	a2(ctg2α−1)		a
H2=		, H=		p{ctg2α
	4		2

masz obliczone a i H..liczymy V..............

sla1: Tam coś zginęło na końcu H= √ctg2α−1

sla1: masakra to pisanie wzorków...

sla1: kurka..H= √ctg²α−1...mam nadzieję, ze wszystko ok

sla1: zad 2 nie mam siły, w oczach mi się dwoi...spróbuj podobnie, uzależnić wszystko od krawędzi a i kąta α. pzdr

sla1: w zad 1 nie krawędzie boczne tylko krawędzie podstawy... ale to nic nie zmienia

koń rafał: Dzięki a potrafi ktoś rozwiązać to zadanie? Podstawą graniastosłupa prostego jest sześciokąt foremny o boku a. Mniejsza i większa przekątna graniastosłupa, wychodzące z jednego wierzchołka, tworzą ze sobą kąt α. Wyznacz objętość tego graniastosłupa.