MOŻE KTOŚ ZAJRZEĆ?
Elka: MoŻE KTOŚ ZAJRZEĆ I ROZWIĄZAĆ

NIE POTRAFIĘ...:(
Oblicz objętość czworościanu ABCD , jeżeli I AB I = 2 cm , I AC I = I AD I = I BC I = I
BD I = 3 cm, a I CD I = 5cm.
9 kwi 18:35
Basia: Podbijam. Kto rozwiąże ?
9 kwi 20:32
...: 

9 kwi 21:29
Mariusz: czy wysokosć ostrosłupa będzie w środku okręgu opisanego na podstawie

9 kwi 21:31
b.: Tu jest dużo trójkątów równoramiennych, co upraszcza sprawę...
...można zrobić np. tak:
niech E będzie środkiem AB. Możemy łatwo policzyć długość |DE| (rozważając trójkąt ABD)
oraz |CE| (rozważając ABC). Spodek wysokości czworościanu opuszczonej z D leży na
odcinku CE.
Mamy trójkąt CED, w którym znamy długości wszystkich boków. Możemy więc policzyć długość
wysokości opusczonej z D, która jest równa wysokości czworościanu...
Idę o zakład, że Bogdan zrobi prościej

9 kwi 21:35
Basia: Nie wiem ! Mam problem z tym zadaniem !
9 kwi 21:36
Basia: Prościej chyba się nie da ! Gratuluję b.

9 kwi 21:39
Mariusz: świetnie rozwiązane

Gratulacje

9 kwi 21:42
b.: He he, ale w tym moim ,,rozwiązaniu'' nie ma żadnych rachunków

9 kwi 21:46
Basia: No rachunki to "małe piwo". Wysokości DE i CE tr.równoramiennych z Pitagorasa.
Pole ECD z Herona. Stąd i "zwykłego" wzoru na pole wysokość DD1.
9 kwi 21:50
Basia: b. zajrzyj jeszcze do
13381. Z kątami dwuściennymi jestem zdecydowanie "na bakier".
9 kwi 21:51
xpt: O! To znaczy Basiu, że Ty czegoś nie wiesz ? ;)
9 kwi 22:15
AnŻ: A na moje oko wychodzi trapez...
9 kwi 23:01
AnŻ: trapez równoramienny
9 kwi 23:02
Basia: Nienawidzę kątów dwuściennych ! Ja ich po prostu nie widzę !
9 kwi 23:04
Basia: Jaki trapez ? Tu nie ma żadnego trapezu !
9 kwi 23:06
Bogdan:
Dzień dobry.
Nikt jeszcze nie podał rozwiązania zadania, więc nie można na razie szukać prostszych
rozwiązań.
Podałeś b. ścieżkę dostępu do rozwiązania, zresztą przy tej liczbie i rodzaju
danych ta ścieżka narzuca się. Sądzę, że jest to najlepsza ścieżka, diabeł jednak jak
zwykle tkwi w szczegółach. Tym szczegółem jest wysokość H ostrosłupa. Najprostsze
wyznaczenie długości tej wysokości będzie jednocześnie najprostszym rozwiązaniem
zadania.
Jak więc najprościej wyznaczyć długość H?
Proszę o przedstawianie wszystkich obliczeń.
10 kwi 12:17
Coma13: Trójkąt ABC w podstawie ma identyczne wymiary jak ściana boczna ABD... policzę więc
wysokość podstawy ( "b." zaproponował żeby środek AB chyba oznaczać jako E) więc liczymy
z Pitagorasa trójkąt EBC → hAB2+(AB2)2=32
hAB2 = 32 − 12 = 8 ⇒ hAB = 2√2
Dostajemy trójkąt równoramienny CED którego pole możemy policzyć P=CE*H/2 =
CD*DE*sin(CDE)/2 ⇒ CE=ED a CD=5 otrzymujemy H=5*sin(CDE)
sinus kąta (CDE) obliczymy z cosinusa, którego policzymy z twierdzenia cosinusów...:
(2√2)2 = (2√2)2 + 52 − 2*5*2√2cos(CDE)
⇒ 0 = 25 − 20√2cos(CDE)
⇒ cos(CDE) = −25/−20√2
⇒cos(CDE) = 5/(4√2) = 5√2/8
sin2(CDE) = 1 − cos2(CDE) = 1 − 50/64 = 14/64
sin(CDE) = √14/8
H=5*sin(CDE)= 5√14/8
....poprawcie mnie jeśli się myle
10 kwi 13:25
Coma13: bo jeżeli H mam dobrze to pole podstawy można zapisać z Herona i V=1/3 * Pp * H
10 kwi 13:29
Bogdan:
Coma13 − Wynik jest dobry, ale można wyznaczyć długość H prościej, bez
stosowania miar kątów i bez trygonometrii.
Pole podstawy nie potrzeba obliczać z wzoru Herona, bo masz długości AB i EC.
10 kwi 13:38
Coma13: No z polem podstawy to prawda ze mam wysokość... a jak można policzyć to H prościej?
10 kwi 13:43
Bogdan:
Na razie nie podam propozycji prostszego wyznaczenia długości H, bo chcę zobaczyć
rozwiązania innych, może wśród nich będzie to najprostsze.
Zaręczam jednak, że jest prosty sposób na wyznaczenie długości H i w Twoim Como13
rozwiązaniu między wierszami można ten sposób znaleźć.
10 kwi 13:52
Coma13: szczerze nie wiem ale za jakiś czas zobaczę co wymyśliłeś... ;−)
10 kwi 14:09
Coma13: Bogdanie

widzisz że nie ma innych propozycji...wiec mógłbyś napisać jak można
skrócić to rozwiązanie.... będę bardzo wdzięczny
10 kwi 19:10
Zajączek wielkanocny: przyniósł prezent
Comie i
Bogdanowi
h
ABC = CC
1 =
√9−1 =
√8 = 2
√2
h
ABD = DC
1 =
√9−1 =
√8 = 2
√2
C
1C
2 wysokość CC
1D wyprowadzona z C
1
| | 25 | | 32−25 | | √7 | |
|C1C2|=√8− |
| = √ |
| = |
| |
| | 4 | | 4 | | 2 | |
| | 1 | | 5√7 | |
PCC1D = |
| *5*U{√7{2} = |
| |
| | 2 | | 4 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Wesołych świąt !
11 kwi 08:49
Coma13: no tez tak można... dzięki

11 kwi 12:37
Bogdan:
Dziękuję
zajączku wielkanocny.
Twoje obliczenia można uprościć.
Przyjmując oznaczenia
zajączka wielkanocnego:
C
1 − środek krawędzi AB
C
2 − środek krawędzi CD
|C
1C
2| =
12√7
|C
1C| = 2
√2
oraz
H − wysokość ostrosłupa opuszczona z wierzchołka D na podstawę ABC.
Nie potrzeba obliczać pola trójkata C
1CD, wystarczy stwierdzić:
|C
1C|*H = |CD|*|C
1C
2| czyli 2
√2H = 5 *
12√7 stąd H =
5√74√2
To jest odpowiedź
Comie13 o sposobie wyznaczenia długości H.
Wróćmy do treści zadania. mamy wyznaczyć objętość podanego czworościanu.
Nie chciałbym
b., żebyś przegrał zakład. Można obliczyć objętość tego
czworościanu bez wysokości H. Nie potrzeba wyznaczać długości H i można
obliczyć objętość czworościanu. Potrzebna do objętości wysokość (i to nie jedna,
ale nie H) jest już podana w zadaniu. Istnieje więc inny i prostszy sposób na
obliczenie objętości czworościanu. Na razie jednak wstrzymam się z podaniem
tego sposobu i zapraszam wszystkich do jego odkrycia. Przedstawię rozwiązanie
tego zadania nowym sposobem po świętach. Życzę miłej i odkrywczej zabawy.

11 kwi 12:42
Coma13: Bogdan

mógłbyś przegrać...Zajączek by się ucieszył przynajmniej, nie można go zasmucać
w czasie świąt

11 kwi 12:47
Bogdan:
Ja się z nikim nie zakładałem, więc nie przegram. Przegrałby ten, kto założyby się
z b..
A swoją drogą, to niezła frajda nie tyle rozwiązywać zadania, co znajdować najprostsze
rozwiązania.
11 kwi 13:07
Coma13: b. rozpisał nieformalny konkurs na najprostsze rozwiązanie...jak dla mnie nadal
najprostszym jest moje, gdyż...nie wymaga myślenia tylko przepisywania i podstawiania do
wzorów...ale napisane jest "szukajcie a znajdziecie"

11 kwi 13:11
Bogdan:
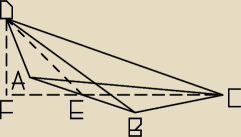
Dzień dobry.
Zobowiązałem się przedstawić najprostsze rozwiązanie zadania po świętach.
Mamy wyznaczyć objętość V czworościanu, w którym:
|AB| = 2, |AC| = |BC| = |AD| = |BD| = 3, |CD| = 5.
|ED| = |EC| = 2
√2
Nasz czworościan wygląda mniej więcej tak, jak na tym rysunku.
Kąt DEC przy podanych długościach krawędzi jest rozwarty, chociaż dla wyznaczenia
objętości V czworościanu nie ma to znaczenia.
Spodek F wysokości DF czworościanu leży na prostej zawierającej wysokość EC
podstawy ostrosłupa.
Krawędź AB jest prostopadła do odcinka EC.
P
ΔDEC =
54√7 to pole powierzchni trójkata DEC będącego przekrojem ostrosłupa
wyznaczone wzorem Herona:
P
ΔDEC =
√ (2√2 + 5/2) * (5/2) * (5/2) * (2√2 − 5/2) =
54√7
Można też wyznaczyć wartość tego pola tak zrobił to
zajączek wielkanocny.
Płaszczyzna zawierająca trójkąt DEC jest prostopadła do płaszczyzny zawierającej
podstawę ostrosłupa ABC.
|AB| = 2 to długość krawędzi podstawy ostrosłupa
Objętość czworościanu
V = 13 * PΔDEC * |AB| =>
V = 13 * 54√7 * 2 = 56√7
Jak widzimy, nie było potrzeby wyznaczania długości wysokości ostrosłupa DF, bo rolę
podstawy ostrosłupa spełnił tu trójkąt DEC, a rolę wysokości − krawędź AB.

Tak zresztą można wyznaczać objetości innych czworościanów. Trzeba wyznaczyć
pole powierzchni
PΔ określonego przekroju ostrosłupa i wziąć do obliczeń
długość tej krawędzi
a czworościanu, która jest prostopadła do wybranego przekroju:
V = 13 * a * PΔ
14 kwi 18:53
 NIE POTRAFIĘ...:(
Oblicz objętość czworościanu ABCD , jeżeli I AB I = 2 cm , I AC I = I AD I = I BC I = I
BD I = 3 cm, a I CD I = 5cm.
NIE POTRAFIĘ...:(
Oblicz objętość czworościanu ABCD , jeżeli I AB I = 2 cm , I AC I = I AD I = I BC I = I
BD I = 3 cm, a I CD I = 5cm.





 Gratulacje
Gratulacje 


 widzisz że nie ma innych propozycji...wiec mógłbyś napisać jak można
skrócić to rozwiązanie.... będę bardzo wdzięczny
widzisz że nie ma innych propozycji...wiec mógłbyś napisać jak można
skrócić to rozwiązanie.... będę bardzo wdzięczny


 mógłbyś przegrać...Zajączek by się ucieszył przynajmniej, nie można go zasmucać
w czasie świąt
mógłbyś przegrać...Zajączek by się ucieszył przynajmniej, nie można go zasmucać
w czasie świąt 

 Dzień dobry.
Zobowiązałem się przedstawić najprostsze rozwiązanie zadania po świętach.
Mamy wyznaczyć objętość V czworościanu, w którym:
|AB| = 2, |AC| = |BC| = |AD| = |BD| = 3, |CD| = 5.
|ED| = |EC| = 2√2
Nasz czworościan wygląda mniej więcej tak, jak na tym rysunku.
Kąt DEC przy podanych długościach krawędzi jest rozwarty, chociaż dla wyznaczenia
objętości V czworościanu nie ma to znaczenia.
Spodek F wysokości DF czworościanu leży na prostej zawierającej wysokość EC
podstawy ostrosłupa.
Krawędź AB jest prostopadła do odcinka EC.
PΔDEC = 54√7 to pole powierzchni trójkata DEC będącego przekrojem ostrosłupa
wyznaczone wzorem Herona:
PΔDEC = √ (2√2 + 5/2) * (5/2) * (5/2) * (2√2 − 5/2) = 54√7
Można też wyznaczyć wartość tego pola tak zrobił to zajączek wielkanocny.
Płaszczyzna zawierająca trójkąt DEC jest prostopadła do płaszczyzny zawierającej
podstawę ostrosłupa ABC.
|AB| = 2 to długość krawędzi podstawy ostrosłupa
Objętość czworościanu
V = 13 * PΔDEC * |AB| => V = 13 * 54√7 * 2 = 56√7
Jak widzimy, nie było potrzeby wyznaczania długości wysokości ostrosłupa DF, bo rolę
podstawy ostrosłupa spełnił tu trójkąt DEC, a rolę wysokości − krawędź AB.
Dzień dobry.
Zobowiązałem się przedstawić najprostsze rozwiązanie zadania po świętach.
Mamy wyznaczyć objętość V czworościanu, w którym:
|AB| = 2, |AC| = |BC| = |AD| = |BD| = 3, |CD| = 5.
|ED| = |EC| = 2√2
Nasz czworościan wygląda mniej więcej tak, jak na tym rysunku.
Kąt DEC przy podanych długościach krawędzi jest rozwarty, chociaż dla wyznaczenia
objętości V czworościanu nie ma to znaczenia.
Spodek F wysokości DF czworościanu leży na prostej zawierającej wysokość EC
podstawy ostrosłupa.
Krawędź AB jest prostopadła do odcinka EC.
PΔDEC = 54√7 to pole powierzchni trójkata DEC będącego przekrojem ostrosłupa
wyznaczone wzorem Herona:
PΔDEC = √ (2√2 + 5/2) * (5/2) * (5/2) * (2√2 − 5/2) = 54√7
Można też wyznaczyć wartość tego pola tak zrobił to zajączek wielkanocny.
Płaszczyzna zawierająca trójkąt DEC jest prostopadła do płaszczyzny zawierającej
podstawę ostrosłupa ABC.
|AB| = 2 to długość krawędzi podstawy ostrosłupa
Objętość czworościanu
V = 13 * PΔDEC * |AB| => V = 13 * 54√7 * 2 = 56√7
Jak widzimy, nie było potrzeby wyznaczania długości wysokości ostrosłupa DF, bo rolę
podstawy ostrosłupa spełnił tu trójkąt DEC, a rolę wysokości − krawędź AB.
 Tak zresztą można wyznaczać objetości innych czworościanów. Trzeba wyznaczyć
pole powierzchni PΔ określonego przekroju ostrosłupa i wziąć do obliczeń
długość tej krawędzi a czworościanu, która jest prostopadła do wybranego przekroju:
V = 13 * a * PΔ
Tak zresztą można wyznaczać objetości innych czworościanów. Trzeba wyznaczyć
pole powierzchni PΔ określonego przekroju ostrosłupa i wziąć do obliczeń
długość tej krawędzi a czworościanu, która jest prostopadła do wybranego przekroju:
V = 13 * a * PΔ