Czy mógłby ktoś mi pomóc?? Marchewcia: BŁAGAM O POMOC! ! ! masakra z tymi zadaniami Zad. W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe S, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę α. Ostrosłup ten przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.

Basia: Rozwiązuję

Eta: ok

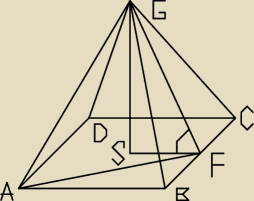Coma13: może będziemy się do czegoś odnosić

Coma13: AB = a AF² = a² + (a/2)² = 5/4 a² czyli AF=√5a/2

xpt: Coma13 − zanim Basia zobaczy Twój rysunek to już napisze rozwiązanie.

Coma13: a² = S ⇒ a=√S ⇒ AF=√5S/2

Coma13: a może była zajęta czyms innym w tym czasie.... ;−D

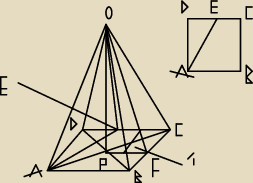Basia: dane: S,α kąt 1 to α Twój przekrój to trójkat AEO AB=BC=CD=AD=a P_p=a² a² = S a=√S −−−−−−−−−−−−−−−

	a		√S
DE =		=
	2		2

z tw.Pitagorasa

	√S		S		5S
AE2 = AD2 + DE2 = a2 + (		)2 = S +		=
	2		4		4

	√5S
AE =
	2

==================== OE = OF

	a2
cosα =
	OF

	a
OE=OF =
	2cosα

	√S
OE =
	2cosα

==================== kąt AEO = kąt PFO = α

	AE*EO*sinα
P =
	2

	√5S   √S   * *sinα 2   2cosα
P =
	2

	S√5sinα		S√5*tgα
P=		=
	8cosα		8

Eta: Basia wytłumacz mi , dlaczego przy obliczaniu pola przekroju wzięłaś ten sam kąt α w/g mnie to nie jest ten sam kąt

Basia: Bo mi się rysunek w oczach zamazał ! Jasne, że nie jest ! Czyli jednak trzeba liczyć OE = OF i potem z wzoru Herona. Tak chciałam od początku, ale to wredne rachunki.

Basia: AO = BO OE = OF juz policzone

Eta: No właśnie Ja liczyłam ze wzoru Herona r−ki paskudne! wiesz , ze łatwiej ze wzoru cosinusów wyliczyłam cos np β a póżniej sin β i wtedy wzór na pole z sinusem β wtedy mniej koszmarne obliczenia

Basia: albo z tej zależności między katem nachylenia krawędzi bocznej i ściany bocznej, której nie pamietam

Coma13: tzn pocieszenie jest takie ze na maturze nikt mi nie będzie kazał upraszczać wyniku.. można więc wszystko zapisać Heronem nie wymnażając... ;−)

Eta: Ok więc niech tak pozostanie. bo rachunki koszmarne niestety Rozumowanie prawidłowe!

Basia: to jest tak: ostr.prawidłowy; podstawa n−kąt; α − kąt nachylenia ściany bocznej do podst. β − kat nachylenia krawędzi bocznej do podst.

	π
cos		= tgα*ctgβ
	n

tutaj

	π
cos		= tgα*ctgβ
	4

√2		tgα
	=
2		tgβ

	2tgα		2√2tgα
tgβ =		=		= √2tgα
	√2		2

β to kat PAO

	PO
tgβ =
	d2

√2tgα = ^2PO_a√2 2PO = 2atgα PO = atgα = √Stgα

	d2		2a2		S
AO2 = PO2 + AP2 = Stg2α +		= Stg2α +		= Stg2α +		=
	4		4		2

U{S{2tg²α+1)}{2}

	√S(2tg2α+1)		√2S(2tg2α+1)
AO =		=
	√2		2

no i teraz albo z Herona, albo tak jak piszesz wyznaczyć kąt AEO z tw.cosinusów tak czy owak koszmar

Coma13: ja mam ze swojego rysunku.. GF= pierwiastek z (4S+tg²S)/4 i AG=pierwiastek z (8S+tg²S)/4

Coma13: dobra nie liczę już nic z tego bo się zgubiłem ze 100 razy już....

Eta: Ja liczyłam tak: ze wzoru cosinusów kąt E = β między AE i EO

a2(1+cos2α)
	=5a24 +a24cos2α− 2a√52*a2cosα*cosβ
4cos2α

po uporzadkowaniu ¹_cos²α +1= 5 +¹_cos²α − ^2√5_cosα*cosβ to:cosβ=^2√5*cosα₅ teraz sinβ= √1−cos²α po uporzadkowaniu: ( nie chce mi sie juz tyle pisać mamy:sinβ=√5−4cos²α *√5/5 teraz do wzoru na pole przekroju: P=¹₂*^a√5₂*^a_2cosα* √5−4cos²α*^√5₅ P= ^5a2_8cosα*√5 −4cos²α a² = S to P= ^S_8cosα *√5 − 4cos²α nie jestem pewna czy się nie pomyliłam w rachunkach!

Basia: Nie sprawdzam ! Wierzę Ci na słowo ! To obłęd !

Eta: Oczywiście że obłęd ! W imię czego takie zadanka podawać Nie rozumiem tego?

Basia: Dobranoc Eto ! Zdrowych i wesołych świąt. Mnie już chyba aż do wtorku nie będzie. No może z doskoku.

Basia: Policzyłam to jeszcze raz od początku do końca, bo mi spokoju nie dawało. Oto obliczenia. AD=a

	a
DE=
	2

	a2		4a2+a2		5a2
AE2 = AD2 + DE2 = a2 +		=		=
	4		4		4

	a√5
AE =
	2

	a
PF =
	2

	PF
cosα=
	OF

	PF
OF =
	cosα

	a
OF =
	2cosα

OE = OF

	a
OE =
	2cosα

	OP
tgα=
	PF

OP = PF*tgα

	a*tgα
OP =
	2

	2a2		a2tg2α		a2(2+tg2α)
OA2 = AP2 + OP2 =		+		=
	4		4		4

	a*√2+tg2α
OA =
	2

kąt AEO = β z tw.cosinusów OA² = AE² + OE² − 2*AE*OE*cosβ

a2(2+tg2α)		5a2		a2		a√5		a
	=		+		− 2*		*		*cosβ
4		4		4cos2α		2		2cosα

a2(2+tg2α)		5a2		a2		a2√5
	=		+		−		*cosβ /:a2
4		4		4cos2α		2cosα

2+tg2α		5		1		√5
	=		+		−		*cosβ
4		4		4cos2α		2cosα

√5		5		1		2+tg2α
	*cosβ =		+		−
2cosα		4		4cos2α		4

√5		5cos2α + 1 − (2+tg2α)*cos2α
	*cosβ =
2cosα		4cosα

	(5cos2α + sin2α + cosα − 2cos2α − sin2α
cosβ =
	2√5cosα

	√5*4cosα
cosβ =
	2*5*cosα

	2√5*cosα
cosβ=
	5

	4*5*cos2α		4cos2α
sin2β = 1−cosβ = 1 −		= 1−
	25		5

	5 − 4cos2α
sin2β =
	5

	√5*(5−4cos2α)
sinβ=
	5

	1
P =		*AE*OE*sinβ
	2

	1		a√5		a		√5*(5−4cos2α)
P =		*		*		*
	2		2		2cosα		5

	a2√5−4cos2α
P =
	8cosα

P = ^{S*√5−4cos2α}_8cosα

Basia: Wesołych Świąt

tim: Wesołych!