Zadanko borys: Dany jest okrąg o równaniu x²+y²−2x+2y−3=0. Wyznacz kąt pod jakim przecinają się styczne poprowadzone do okręgu O₁ z punktu P=(−2;0).

borys: Pomoże ktoś? Proszę, zalezy mi

Aga1: Najpierw musisz wyznaczyć te styczne. Równanie stycznej przechodzącej przez P jest postaci y=a(x+2) y=ax+2a Rozwiąż układ równań okrąg i prosta Prosta z okręgiem mają jeden punkt wspólny gdy Δ=0

borys: Czemu równanie stycznej ma postać y=a(x+2) ? Nie rozumiem skąd to się wzięło

grizzli: Wytłumaczcie mi proszę !

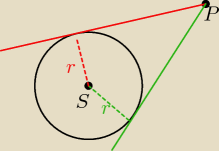
Gustlik: Podstawiasz współrzędne P=(−2, 0) do równania prostej y=ax+b i wyliczasz b: 0=a*(−2)+b 0=−2a+b b=2a i podstawiasz do funkcji liniowej: y=ax+2a Teraz można to rozwiązać tak − bez układu: x²+y²−2x+2y−3=0

	A		−2
a=−		=−		=1
	2		2

	B		2
b=−		=−		=−1
	2		2

r=√a²+b²−C=√1²+(−1)²−(−3)=√1+1+3=√5 Środek okręgu S=(1, −1), promień r=√5 Przekształcam równanie prostej do postaci ogólnej: y=ax+2a 0=ax−y+2a ax−y+2a=0 Liczę odległość środka okręgu d tej prostej i przyrównuję do promienia − warunek styczności:

	|a*1−(−1)+2a|		|3a+1|
d=		=
	√a2+(−1)2		√a2+1

|3a+1|
	=√5 /()2
√a2+1

(3a+1)2
	=5 /*(a2+1)
a2+1

9a²+6a+1=5a²+5 4a²+6a−4=0 Δ=100, √Δ=10

	1
a1=−2, a2=
	2

Proste styczne mają równania:

	1
y=−2x−4 i y=		x+1
	2

Zatem α=90^o, bo widać, że współczynniki kierunkowe spełniają warunek na prostopadłość prostych.

Aga1: lub x²+y²−2x+2y−3=0 y=ax+2a x²+(ax+2a)²−2x+2(ax+2a)−3=0 x²+a²x²+4a²x+4a²−2x+2ax+4a−3=0 (1+a²)x²+(4a²+2a−2)x+4a²+4a−3 Δ=(4a²+2a−2)²−4(1+a²)(4a²+4a−3) Δ=16a⁴+4a²+4+16a³−16a²−8a−16a²−16a+12−16a⁴−16a³+12a²=−16a²−24a+16 Δ=0⇔ −16a²−24a+16=0 //:−4 Δ=2a²+3a−2=0 Δ_a=9+16 √Δ_a=5

	1
a1=−2, a2=
	2

a₁*a₂=−1⇒proste są prostopadłe.