funkcja kwadratowa eddy: eddy: Sporządź wykres funkcji: −3 dla x nal. (−∞;−4] f(x)= −x+2 dla x nal. (−4;1) √x dla x nal. [1;∞) Wyznacz ZW i miejsca zerowe oraz pkt. przecięcia z OY. Opisz przedziały monotoniczności. Dla jakich argumentów funkcja przyjmuje wartości +. Dla jakich −. Proszę o pomoc!

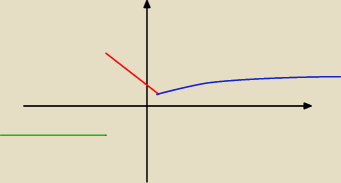
asdf: takie cos? fajnie jakby ktoś to sprawdził, też jestem ciekawy

asdf: ?

eddy: raczej nie chodzi o to

Aga1: Wykres tej funkcji dobrze narysowany. Zw={−3}∪<1,∞) Brak miejsc zerowych, funkcja jest stała dla x∊(−∞,−4> malejąca dla x∊(−4,1) i rosnąca dla x∊<1,∞) f(x)>0 dla x∊(−4,∞) f(x)<0 dla x∊(−∞,−4>

asdf: no i git

eddy: dzięki