Zadanko do matury... :(
Kasia: Możecie mi pomóc? Nie wychodzi i o to takie zadanko:
Podstawą graniastosłupa prostego jest równoległobok o bokach długości 2 i 4 oraz kącie
ostrym o mierze 60 stopni. Krótsza przekątna graniastosłupa tworzy z podstawą kąt o
mierze 30 stopni. Oblicz pole powierzchni graniastosłupa...
9 kwi 13:46
Bogdan:
Oblicz najpierw długość krótszej przekątnej równoległoboku.
9 kwi 14:07
Kasia: mało mi to pomogło....
9 kwi 16:43
xpt:
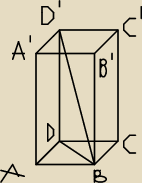
Rysunek może się przydać, jednak rozwiązanie zostawiam Bogdanowi bo pewnie się już za to
zabrał
9 kwi 16:58
xpt:
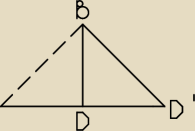
Dobra − Bogdan gdzie uciekł, to ja przejmuję "jego" zadanie
Z obliczeniem pola podstawy sobie poradzisz ?
Wysokość obliczasz, z własnosci trojkąta równobocznego.
Trójkąd D B D' jest połową trójkąta równobocznego (patrz:rysunek).
Wysokość tego graniastosłupa, to połowa odcinka |BD|, który już obliczyłaś (krótsz a
przekątna podstawy).
| | a√3 | | 1 | |
Z wzoru h= |
| wyznaczasz ile wynosi odcinek |DD'| (czyli |
| a). |
| | 2 | | 2 | |
Dalej chyba sobie poradzisz?
9 kwi 17:24
Bogdan:
Dzięki xpt. Naprawiam szafki w kuchni, a Kasia długo nie odpowiadała, więc nie
zaglądałem tutaj. Pozdrawiam
9 kwi 17:33
Kasia: dzięki chłopaki, to znaczy że nie jestem aż taka ciemna bo w ten właśnie sposób
rozwiązywałam te zadanko... tylko że odpowiedź w "odpowiedziach" jest podobno inna, ale
trzymajmy sie wersji że Pan Kiełbasa sie pomylił
Pozdrawiam
9 kwi 20:22
Bogdan:
Kasiu, podaj swoje rozwiązanie. Sprawdzimy Ciebie i p. Kiełbasę
9 kwi 20:26
tim: pana Kiełbasę
9 kwi 20:27
Bogdan:
tim, napisałem p. Kiełbasę, co oznacza pana Kiełbasę
9 kwi 20:29
tim: No wiem
, ale fajne nazwisko
9 kwi 20:31
Bogdan:
takie wielkanocne
9 kwi 20:31
tim: pani Babeczka <−− moja nauczycielka techniki
9 kwi 20:33
Bogdan:
O! Też wielkanocna pani
9 kwi 20:35
xpt: A ile CI wyszło ? Bo mi wyszło 8 jak policzyłem,
a z kiełbasy mi wychopdzi, ze powinno być 8(3−P{3}).
9 kwi 20:37
xpt: 8(3−√3)
9 kwi 20:37
Basia: Mnie wyszło 8(3+√3)
9 kwi 20:43
Basia: Ale zaraz ! Co to ma być krótsza przekątna graniastosłupa ?
9 kwi 20:47
xpt: Basiu dobrze Ci wyszło, ja pomyliłem znaki.
Krótsza przekątna graniastosłupa jest to odpowiednik któtszej przekątnej równoległoboku,
z tym że w trójwymiarze ;)
9 kwi 20:48
Bogdan:
Długość krótszej przekątnej e wyznaczamy z wzopru kosinusów.
e
2 = 4 + 16 − 16*
12 => e = 2
√3
Wysokość H graniastosłupa i przekątna e tworzą trójkąt prostokątny, w którym:
| H | | √3 | |
| = tg30o => H = 2√3* |
| = 2
|
| e | | 3 | |
| | √3 | |
Pole powierzchni P = 12*2 + 2*2*4* |
| = 24 + 8√3 = 8(3 + √3) |
| | 2 | |
9 kwi 20:51
tim: kosinusów? xD
9 kwi 20:52
Basia: O.K. Czyli 30 to kąt między przekątną gr. i d1.
9 kwi 20:52
Basia: Co Cię dziwi Tim ?
9 kwi 20:53
Bogdan:
pole równoległoboku PR = a*b*sinα
a, b − długości boków,
α − miara kąta między bokami
9 kwi 20:54
xpt: A! Już wiem gdzie mam bląd, to co ja wyliczyłem to nie byyło pole powierzchni tego
graniastosłupa :P
Przypomniało mi się nawet, ze ten sam błąd zrobiłem w zeszłym roku, jak to samo zadanie
liczyłem po raz pierwszy :P
Albo to było bardzo podobne zadanie i podobny błąd zrobiłem :P
9 kwi 20:54
Bogdan:
tim, znani Ci wzór Pitagorasa jest szczególnym przypadkiem opisanym
przez wzory kosinusów, które nazywane są również wzorami Carnota
9 kwi 20:57
tim: Tak, jestem zdziwiony
9 kwi 20:58
xpt: tw. cosinusów jest po prostu prawdziwe dla dowolnego trójkąta, a nie tylko tego
prostokątnego ;)
9 kwi 20:59
Kasia: no teraz juz i ja wiem gdzie błąd popełniłam... Dzięki wielkie i wesołych świąt
10 kwi 07:50