sześcian przecięty płaszczyzną qwerty: sześcian o krawędzi a przecięto płaszczyzną przechodzącą przez przekątną ściany i nachyloną do tej ściany pod katem 30 stopni. Oblicz stosunek objętości brył, na które płaszczyzna przekroju podzieliła sześcian.

qwerty:

	6√6+1
Odpowiedź: k=
	215

Aga1:

	a√2
IOCI=x=
	2

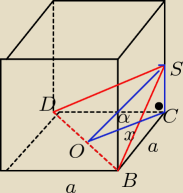
BCDS jest czworościanem o podstawie BCD i wysokości h= ICSI

	h
tgα=
	x

	√3		a√2		a√6
h=		*		=
	3		2		6

	1		1		a√6		a3√6
V1=VABCDS=		*		a2*		=
	3		2		6		36

	a3√6		36a3−a3√6
V2=Vsześcianu−V1=a3−		=
	36		36

V2
	=
V1

dokończ

Aga1: Oblicz

V1
	, a otrzymasz wynik taki, jaki podałeś/aś.
V2

qwerty: super, wielkie dzięki największym problemem okazało się poprawne zaznaczenie kata α

Krzysztofek: Witam,mógłby ktoś wytłumaczyć dlaczego przekrój wygląda akurat tak? ja myślałem,że jak płaszczyzna przechodzi przez przekątną śćiany to jej wierzchołek będzie w punkcie C'

Aga1.: Jeśli przekrój przechodzi przez wierzchołek C^', to

	a
tgα=
	1   a√2 2

Wtedy kąt α≈54⁰

Krzysztofek: Nadal mi to jakoś niczego nie rozjaśniło

Mila: Krzysztofek, jeśli zrobisz sobie kostkę sześcienną z ziemniaka, to przecież możesz różnie odkroić naroże.