1.Zbiór wszystkich liczb x, których odległość od liczby 7 na osi liczbowej nie j Sławek.: 1.Zbiór wszystkich liczb x, których odległość od liczby 7 na osi liczbowej nie jest mniejsza niż 4, jest opisany nierównością: a)|x−7|>4 b)|x+7|>4 c)|x−7|≥4 d)|x+7|≥4 Mi wychodzi a a ponoć jest jest c. Dlaczego?

Sławek.: a z tym jest mi ktoś w stanie pomóć?

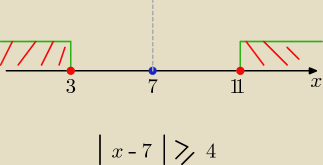
Eta: odległość nie jest mniejsza od 4 czyli jest ≥ 4 odp c)

Sławek.: kurde źle przepisałem polecenie, miało być JEST NIE MNIEJSZA niż 4

Eta: No czyli musi być ≥4

Sławek.: no właśnie. to wg. tego co mi napisałeś odległosć od 7 będzie mniejsza niż 4 bo patrzać od prawej to będzie 8,9,10 a 11 już nie bo należy do tamtego zbioru.

Sławek.: hmm?

Sławek.: wytłumaczycie mi to?

Eta: Wskaż kilka liczb, dla których odległość od 7 jest nie mniejsza niż 4

Sławek.: ale chodzi mi o to, czy ta "odległość" to chodzi o te liczby spełniające tę nierównosć czyli te w zakresie zakreskowanym czy o te w zakresie nie zakreskowanym? (wg. Twojego rysunku)

Eta: W zakreskowanym !

Sławek.: i to wszystko wyjaśnia! Dziękuje ETA!

Sławek.: i to wszystko wyjaśnia! Dziękuje ETA!

Eta: Na zdrowie