Ostrosłupy. Basiek: Bu Mam takie jedno pytanie: Podstawą ostrosłupa ABCDS jest kwadratem ABCD o boku długości 4. Odcinek DS jest jest wysokością ostrosłupa i ma długość 6. Punkt M jest środkiem odcinka DS. Oblicz pole przekroju ostrosłupa płaszczyzną przechodzącą przez krawędź BC podstawy i punkt M.

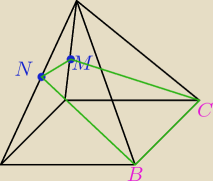
Basiek: Do zadania mamy w odpowiedziach stosowny rysunek: Skąd im się wziął punkt N wyznaczający płaszczyznę? Po co? Dlaczego?

Yay: otrzymasz ostrosup prostokąt...przynajmniej ja to tak nazywam...taki sam jak był w 20którymś zadaniu na podstawowej maturze w tym roku tydzien temu (ten z siatką), Mam nadzieję że pomogłem

DZIADZIA: czesc Basiek ej to chyba nie jest trudne zadanie a Ty masz z nim problem?

Basiek: @Dziadzia, chyba jest.

Yay: niee.....to nie może być ten rysunek. skoro DS jest wysokością to musi być prostopadły do podstawy

DZIADZIA: może dla zmyły dali te punkty N i M...

Basiek: @Yay, ale wiesz, tam jest kąt prosty. Ja tu przerysowałam to mniej−więcej, bo w sumie to... moje pytanie skupia się na punkcie N. Naprawdę nie bardzo rozumiem, co on tu robi −₋

DZIADZIA: Basiek ta próbna co była teraz to był jakis absurd zamkniete zadania to bez liczenia można było robić.Czy czegoś takiego mam się spodziewać na maturze 2012?!

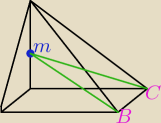
Basiek: Dlaczego nie tak?

Basiek: @Dziadzia, ale ja nie jestem jasnowidzem. Nie wiem.

Mila: "Połóż" sobie tę figurkę na tylnej ściance i krój nożem przez BC, tak aby trafić na środek DS, czyli punkt M.

DZIADZIA: oj widzę że humorek cos nie teges

Yay: ponieważ płaszczyzna jest całą "plytą przechodzącą przez ten ostrosłup. http://pl.wikipedia.org/wiki/Płaszczyzna. Według twojego rysunku jest to fragment w środku ostrosłupa. Płaszczyzna jest nieskończona a oni proszą cie tylko o pole przekroju, czyli o konkretny fragment płaszczyzny. Rozumiesz teraz?

Basiek: Nie rób mi psychoanalizy, bo troszkę Ci nie idzie. @Mila− okeej, to nawet nie chodzi o to, że to N jest tam, gdzie jest. To chodzi o to, że ono coś wyznacza. Czy jeżeli mamy przekrój płaszczyzną jakiejś figury, to muszę ją całą..."przeciąć"? Bo ja bym hm... po prostu wyznaczyła płaszczyznę, nie patrząc na to, czy ona przecina figurę, czy tylko jest w środku... Nie wiem.

Basiek: O, właśnie o to pytałam. Dziękuję. Nie miałam pojęcia.... Teraz jasne.

Basiek: Jeszcze @Yay, gdybyś mi mógł zdradzić dlaczego to jest trapez prostokątny, to byłaby już pełnia szczęścia

Mateusz: Bo ma co najmniej dwa kąty proste widzisz je ?

Basiek: Nie

Yay: własnie miałem napisać że jeżeli moja wyobrażnia dobrze pracuje to bedzie to trapez prostokątny kurde jakbym umiał programowac to bym Ci zrobił prezentacje kurde po prostu musisz sobie wyobrazic tą figurę i zobaczyć w jakim miejscu lezy ten punkt N. Gdy patrzymy na ten ostrosłup z góry widzimi kwadrat a wierzchołek S pokrywa sie z wierzchołkiem D. Teraz idziemy dalej. Krawędź CS pokrywa sie z krawędzią CD a krawędź AS z krawędzią AS. Gdy wyobrazimy sobie punkt M który musi też leżec w tej sytuacji tam gdzie punkty D i S juz atwo powinnaś sobie wyobrazić gdzie jest punkt N

Mila: BC jest prostopadłe do CM bo jest prostopadłe płaszczyzny DCS zatem jest prostopadłe do każdej prostej przechodzącej przez C i leżącej w tej płaszczyźnie.

Basiek: Jesteś genialny O.o

Basiek: Mila bo to chodzi o jakieś twierdzenie właśnie, że jeśli coś, to coś na płaszczyźnie jest prostopadłe. Może wiesz, jak to wpisać w google, żeby to odnaleźć? I w ogóle dzięki Wam Powoli zaczynam łapać. Ale długa droga przede mną jeszcze, jeśli o stereometrię chodzi

rumpek: twierdzenie o trzech prostych prostopadłych

Basiek: Rumpek dzięki. Będę się w to gapić tak długo, aż coś może dotrze do mojej znękanej świadomości. I wiesz co? https://matematykaszkolna.pl/forum/133317.html

rumpek: o jasny gwint

rumpek: dobra biorę się za pisanie jutro tak koło 11−12 podeśle, bo mam dzień wolny pardon za zwłokę

Basiek: Nic się nie dzieje spokojnie, tylko przypominam, bo mam wrażenie, że chyba zapomniałeś

rumpek: dobre wrażenie wczoraj wiedziałem, że dzisiaj mam pisać (napisać to), a jak przyszedłem do domu od razu do łóżeczka i lulu do 18 i zapomniałem

rumpek: dzięki za przypomnienie

Basiek: Nie ma za co. Dzięki za pomoc

Basiek: To może uda mi się dowiedzieć jeszcze tego: Wykaż, że jeżeli podstawą ostrosłupa jest trapez i krawędzie boczne ostrosłupa są równej długości, to podstawa ostrosłupa jest trapezem równoramiennym. I tu moje pytanie: no bo jeśli przyjrzymy się czterem trójkątom, jakie tworzą krawędzie boczne(przeciwprostokątna) oraz wysokość ostrosłupa( przyprostokątna) to wynikałoby z tego, że te trójkąty będą mieć taką samą drugą przyprostokątną.... czyli w zasadzie wynikałoby z tego, że podstawą jest: czworoką, trapez, o przekątnych równej długości przecinających się w połowie− czyli że prostokąt. Gdzie coś pochrzaniłam, może mnie ktoś oświecić? Prooszę.

Aga1: Ostrosłup , o którym mowa w zadaniu jest ostrosłupem prostym, bo wszystkie krawędzie mają tę samą długość Na podstawie ostrosłupa prostego można opisać okrąg, a spodek wysokości znajduje się w środku okręgu opisanego na podstawie.

Aga1: Jeżeli trapez równoramienny nie jest równoległobokiem to można na nim opisać okrąg, bo...

Basiek: Bo jest on trapezem równoramiennym, dziękuję

Aga1: Basiu napisałaś 'masło maślane' bo sumy przeciwległych kątów są równe i mają po 180⁰ stopni.