Wykaż, że powierzchnia boczna stożka jest półkolem. logitech: Kąt rozwarcia stożka ma 60 stopni. Wykaż, że powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem.

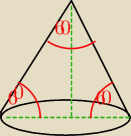
ewa: Skoro kAt rozwarcia stożka jest 60⁰, to w przekroju osiowym mamy trókąt równoboczny o boku 2r, gdzie r −promień podstawy stożka. Zatem tworząca stożka l=2r. Powierzchnia boczna stożka jest zatem wycinkiem koła o promieniu 2r i długości łuku równej obwodowi podstawy czyli 2πr. Obwód całego koła o promieniu 2r wynosi 4πr. Zatem dany wycinek stanowi dokładnie połowę tego koła, co nalezało wykazać

pigor: ... czyli obwód podstawy = 2πr= 2π ^l₂= ¹₂2πl , a to właśnie jest połową obwodu okręgu koła o promieniu l − tworzącej stożka , czyli powierzchnia boczna tego stożka faktycznie jest półkolem c.n.w. . ...