f. kw
invisible: Wykres funkcji kwadratowej f(x)=−x
2+1 ma dwa punkty wspólne z prostą o rownaniu: x=−1, x=1,
y=−1, y=1 takie zadania sa na tej amturze ze ja znowu nie zdam

15 mar 16:40
Basia:
naszkicuj parabolę i te proste, i po krzyku
parabola:
ramiona w dół; wierzchołek W(0,1); miejsca zerowe x1 = −1 i x2 = 1
15 mar 16:49
invisible: nie rozumiem
15 mar 16:53
Basia:
i nie zrozumiesz dopóki nie narysujesz
15 mar 16:58
invisible: narysowalam i co?
15 mar 17:00
Basia:
no to chyba widzisz, która z tych prostych ma z parabolą jeden punkt wspólny, która dwa punkty
wspólne, a która nie ma żadnego
15 mar 17:03
invisible: x=−1 i x=1
15 mar 17:04
Basia:
prosta y = −1 dwa
proste x= −1 i y=1 i x=1 po jednym
a np. prosta y = 2 nie ma żadnego
15 mar 17:05
Basia:
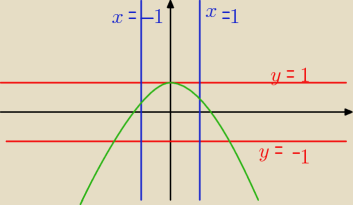
15 mar 17:12
invisible: czyli y=−1

15 mar 17:15
Basia: tak

15 mar 17:23
Aa: pytanie tylko czy invisible wie dlaczego parabola ma skierowane ramiona do dołu
jak obliczyć W
i jak obl. się miejsca zerowe
bz tego nie ma sie z czego cieszyć
15 mar 17:31
invisible: tak wiem dlaczego w dol bo patrzymy na −x i dlatego w dol. 0 i 1 bo −x=0 a 1 to 1 z miejscem
zerowym troche kiepsko

16 mar 08:13
Aga1: To może tak
y=−x
2+1
a=−1,b=0 , c=1
Δ=b
2−4ac=0−4*(−1)*1=4
√Δ=2
x
2=
Lub
−x
2+1=0//* (−1)
x
2−1=0
(x−1)(x+1)=0
x−1=0 lub x+1=0
x=1 lub x=−1.
16 mar 08:19
invisible: ale zle to zrobilas bo x1= −0+2/ 2*(−1)=2/−2= −1 a x2=−0−2/2*(−1)=−2/−2=1
16 mar 08:54
Aga1: Może być tak jak Ty zrobiłeś/aś.
Moje obliczenia są też ok.
16 mar 10:17
invisible: as

ok dzieki

16 mar 10:45





 ok dzieki
ok dzieki 